Вопрос 17) Безвихревое стационарное обтекание тел жидкостью, газом.

] В движ-ся жидк-ти есть тело произв формы

Расчитаем распределение скорости в окрестности обтекаемого тела. Течение жидкости можно описать векторным полем скоростей : кажд точке прост-ва в этом случае ставится в соответствие вектор Ū (m,t)

(в стационарном случае V(m) только от коорд-ты)

Пусть rot Ū=0 в каждой точке области, такие течения безвихревые. Еще одно ур-ние для скорости Ū выведем из закона сохранения масс:

М ысленно выделим в поле скоростей произвол фикс обьем огранич-ный S.

В соотв с з-ном сохр масс для этого объема можно записать

_sŪdS = - _(/t)d (*)

Слева: имеет смысл кол-ва жидкости протекающей через S в единицу времени.

Справа: измен массы ж-ти внутри объема в 1 времени

-массовая плотность ж-ти .

Знак “ - “ соответствует положит внешней нормали . Применяя теор Гаусса получим:

_ [(/t)+div Ū] d=0 . исп теор о среднем имеем :

/t (М*) + div ((M*) Ū(M*))=0 . В силу произв-ти  это соотнош справедливо для любой т. М

В стационарном случае /t=0  div Ū = 0 – ур-ние неразрывности . Для однород поля скоростей =const имеем div Ū=0 т.е. поле соленоидально. Искомое поле удовлетв : {rot U=0  U=grad  ;

{div U=0 ;

1-е ур позвол ввести в обл. ск/поле  наз. потенц-лом

подставим его во 2-е получим : div  grad =0

Итак, решение сводится к ДУ в частных производ относи-тельно . Решений очень много, для выделения единств реш-я соответствующего конкретной постановке задачи необходимы доп условия. В случае обтекания жид-ю тела произвольн ф-мы в кач-ве таковых можно принять поведение вектора U на пов-ти обтекаемого тела и на .

Если пов-ть непроницаемая, то доп усл : U_n_s= 0 

/n_s=0 ; U_n нормальная составляющая скорости

Доп усл на : поле скоростей невозмущено :

Ū()=Ū_  ()=_ . Можно показать что эти доп условия гарантируют единствен реш ур-ния для 

Выведенное ур-ние для  + доп условия гарант-щие единств-ть реш-я образуют модель безвихревого стац-ого обтекания тела жидк-ю. Замечание: если движ газа можно описывать гидродинамическ ур-ями , то всё выше сказанное относ и к обтеканию газом тела

Вопрос 18)Ур-ие теплопроводности, постановка задачи для него.

Рассм тв тело, температура различных точек которого в различные моменты врем описывается функ Т(м, t)

В соответ с законами термодинамики теплота распростр от точек где она выше к точкам где она ниже. Выведем урав, кот удовлетв ф-ция Т(м, t)

Зафикс в теле произв точку М, выберем окрест ∆S

В соответ с гипотезой Фурье кол-во тепла, прошедшее через ∆ S за ∆t пропорционально произведению ∆S∆t и на нормальную производную температурного поля

∆ Q=-k(M)∆S∆t(T/n)

T/n – производная по нормали к ∆ S, направленная в сторону уменьшения температуры

k(M)- коэф пропорцион (коэф теплопров материала)

“ - ” соответствует выбранному направлению нормали

q- скорость теплов потока через единич площадку ∆S

q=-k(T/n)=∆Q / ∆t –закон теплопровод Фурье

Устанав связь между тепл потоком и нормальн произв Отсюда  физич содержание коэф-та теплопров

k- кол-во тепла прошедшее через единич площадку за единицу времени при условии T/n=1

[k]=1 Вт / М*градус

Примеры: Серебро(t=0) k=418

4^х хлористый углерод k=0,0086

Вещ-ва для которых k ≤ 0,23 считаются теплоизолят, остальные вещ-ва - проводники тепла

Выделим в окрестности т. М некоторый объем V ограниченный гладкой пов-тью S

Пусть за ∆t внутри объема прошло кол-во тепла Q.

В соответ с законом Фурье:

На изменение температуры объема V от Т(t₁) до T(t₂)необходимо кол-во тепла:

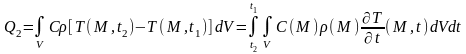
Если в объеме действуют источники тепла с плотностью ρ(М,t), то кол-во тепла:

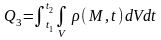
Уравнение баланса тепла для объема V:

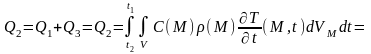
преобразуем объемный интег с помощью теор Гаусса

подставляя в уравнение теплового баланса и объединяя все интегралы получим:

Это равенство справедливо для любого V и отрезка. Поэтому из равенства нулю следует равенство нулю под интегрального выражения

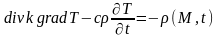
Распредел температур поля в объеме V

– ур-ние теплопровдности k,c,=const ;

∆T-(1/a)(T/t)=f ; (1/a)=c /k ; f = - (/k)

Если температурное поле зависит от двух пространственных координ, то уравн примет вид:

∆ _{x y} T - (1/a)(T/t )=f –двумерное уравн теплопровод

Если температурное поле зависит от одной координ, то уравнение примет вид: ²T/X² - (1/a)(T/t)=f -одномерное уравнение теплопроводности

Можно показать, что такому же уравнению будет удовлетворять концентрация некоторого вещ-ва, распространенного в среде. Это уравнение описывает любой диффузионный процесс. Коэффициент а определяет скорость диффузии.

Ур диффузии имеет  много решений.

Единственное решение соответствующее конкретной постановке задачи выделяется из этого множества заданием дополнительных условий. Для ур диффузии характерными являются начальные и краевые условия.Краевые условия для диффузии описывают способ теплообмена выделенного объема с окружающей средой и заключается в задании поведения искомой функ на границах области. Они бывают след видов:

1) краевое условие первого рода; заключается в задании искомой функции на границе области

T|_S =f(M,t), MS

2) краевое условие второго рода; заключается в задании теплового потока на границе области

(T/n)|_S= f(M,t), MS

3) краевое условие третьего рода; заключается в задании линейной комбинации температуры и потока на границе области

₁T+₂(T/n)|_S= f(M,t), MS

4) начальное условие: температурное поле в начальный момент времени t=0

Это условие несет информацию об источниках тепла, действующих до момента времени t=0

Можно показать, что перечисленные краевые и начальные условия гарантируют единственность решений уравнений теплопроводности