14.Практическое применение уравнения Бернулли (водомер Вентури, трубка Пито).

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим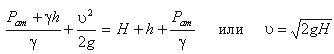

где Н - столб жидкости в трубке Пито.

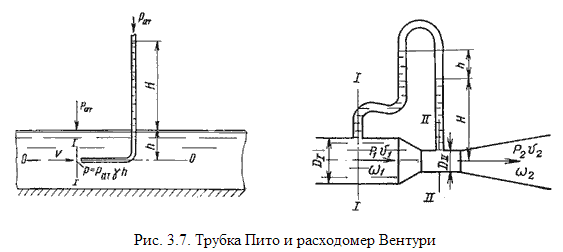
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

или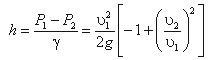

Используя уравнение неразрывности сделаем замену в получено выражении: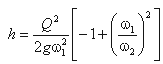 Решая относительно Q, получим 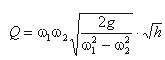Выражение, стоящее перед , является постоянной величиной, носящей название постоянной водомера Вентури. Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

15.Режимы движения жидкости. Критерий Рейнольдса.

Предложение о существовании двух режимов движения жидкости впервые

высказал Д. И. Менделеев в 1880 г., а через 3 года английский физик

Осборн Рейнольдс экспериментально подтвердил существование двух режимов. Они были названы ламинарным и турбулентным.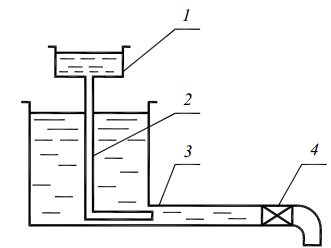 Рейнольдс пропускал водчерез стеклянные трубки разного диаметра, регулируя скорость движения воды краном 4. По тонкой трубке 2 к потоку подводилась окрашенная жидкость из сосуда 4. Опыты показали, что при малых скоростях движения воды в трубке 3 окрашенная жидкость движется в виде тонкой струйки внутри нее, не перемешиваясь с водой (ламинарный режим). После достижения определенной для данных условий опыта скорости движения воды, движение частиц жидкости приобретает беспорядочный характер. Струйка окрашенной жидкости разрушается, размывается, отчего вся вода в трубке окрашивается, наступает турбулентный режим. Таким образом, в ламинарном режиме жидкость движется струйчато или слоисто, без перемешивания. В турбулентном режиме частицы жидкости движутся хаотично, струйки быстро разрушаются. Рейнольдс установил, что критерием режима движения жидкости является безразмерная величина, которая впоследствии была названа числом Рейнольдса Re. В общем случае число Рейнольдса Re определяется по формуле