27. Расчет простых, последовательно соединенных трубопроводов
Последовательный трубопровод состоит из нескольких труб различной длины и различного диаметра, соединённых между собой.
Последовательное соединение трубопроводов. Рассмотрим трубопровод, состоящий из п последовательно соединенных труб различных диаметров. Каждый участок этого трубопровода имеет длину l и диаметр d.
В каждом из этих трубопроводов могут иметься свои местные сопротивления. Течение в жидкости в такой трубе подчиняется следующим условиям:
ь р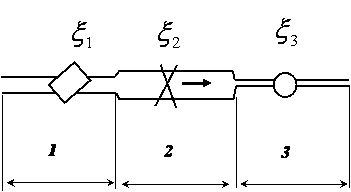
асход
на всех участках трубопровода одинаков,
т.е. 
;
ь потери давления (напора) во всём трубопроводе равны сумме потерь на каждом участке:
При движении жидкости по трубопроводу весь напор Н будет затрачен на преодоление потерь напора по длине.
Полная потеря напора в длинном трубопроводе равна сумме потерь на отдельных участках
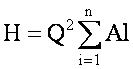
где l — длина участка, м; A— удельное сопротивление участка.
Для гидросистем:
.
С учётом сказанного нетрудно получить уравнение для определения суммарных потерь давления, которое примет вид
,
где 
-
суммарное гидравлическое сопротивление
всего трубопровода.
Величина суммарного сопротивления с учётом ранее полученной формулы для простых трубопроводов составит.
В общем случае выражение, описывающее суммарное гидравлическое сопротивление сложного трубопровода, будет выглядеть:
.
Полученное
уравнение, определяющее суммарные
потери давления, представляет собой
характеристику сложного трубопровода,
которая является суммой характеристик
простых трубопроводов. Это уравнение
позволяет узнать, какие энергетические
характеристики должен иметь источник
энергии, чтобы жидкость могла протекать
по всему трубопроводу. Однако в конечной
точке этой трубы энергия жидкости будет
равна нулю. Если в конце трубы необходимо
иметь какое-то давление 
(например,
чтобы преодолевать нагрузку) к
величине 
нужно
добавить эту величину. Кроме того, т.к.
в общем случае величина скоростного
напора в начале 
и
в конце 
трубопровода
из-за разных диаметров различны,
необходимо добавить и эту разницу
к 
.
В результате энергия, которой должен
обладать источник, должна составлять
.
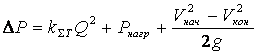28. Расчет простых, параллельно соединенных трубопроводов
Отличительной
особенностью таких трубопроводов
является то, что поток жидкости делится
в одной точке на несколько самостоятельных
потоков, которые позже сходятся в
другой точке. Каждый из этих потоков
может содержать свои местные сопротивления.
Наиболее часто возникающей задачей,
связанной с расчётом таких трубопроводов,
является определение расхода в каждой
ветви. Рассмотрим движение жидкости по
этим трубопроводам, считая, что
потенциальная энергия положения 
много
меньше потенциальной энергии сжатия,
которая определяется давлением, и ею
можно пренебречь. Если считать, что в
местах разветвления и соединения
трубопроводов, обозначенных
буквами н и к, расход 
одинаков,
а давления равны 
и 
,
то можно записать:
Особенность расчета заключается в том, что потери напора в каждой из линий одинаковы и равны разности напоров в узлах а и б.
h1= h2 = h3 = ... = hn = hA - hB=H
Расход через любую из линий, соединяющих точки А и В, может быть записан в виде
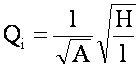
Так как сумма расходов во всех параллельных трубопроводах равна расходу Q до разветвления трубопровода
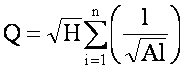
И для гидросистем
”P1, ”P2, ”P3– потери давления в соответствующих ветвях.
Представляя каждую из параллельных ветвей как простой трубопровод, можно записать характеристики каждой ветви:
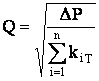
Из приведённых уравнений вытекает следующее важное правило: для построения характеристик параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик каждого из этих трубопроводов при одинаковых ординатах (потерях давления).