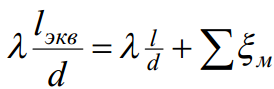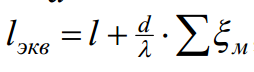25. Истечения через отверстия при переменном напоре

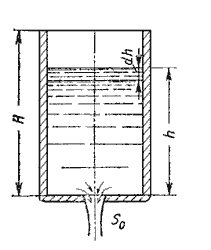
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.5.10).

Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.

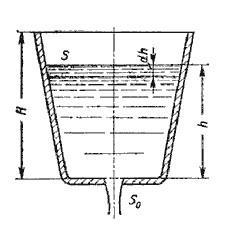
Рис. 5.10. Схема опорожнения резервуара

Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровнеS, площадь отверстия S_о, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:

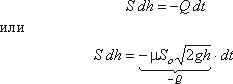
где dh - изменение уровня жидкости за время dt.

Отсюда время полного опорожнения сосуда высотой Н

Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.5.11), следовательно, время его полного опорожнения

Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.

Рис. 5.11. Опорожнение призматического резервуара	Рис. 5.12. Опорожнение непризматического резервуара

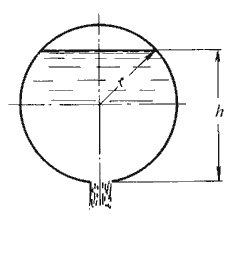
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 5.12) выразим зависимость переменной площади S от h:

где l - длина цистерны; D - диаметр цистерны.

Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h₁ = D до h₂ = 0, получится равным

26. Расчет простых трубопроводов

Основным элементом любой трубопроводной системы, какой бы сложной она ни была, является простой трубопровод. Классическим определением его будет - простым трубопроводом является трубопровод, собранный из труб одинакового диаметра и качества его внутренних стенок, в котором движется транзитный поток жидкости, и на котором нет местных гидравлических сопротивлений. При напорном движении жидкости простой трубопровод работает полным сечением 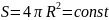. Размер сечения трубопровода, а также его длина являются основными геометрическими характеристиками трубопровода. Основными технологическими характеристиками трубопровода являются расход жидкости в трубопроводе и напор. Большинство других характеристик простого трубопровода являются, не смотря на их важность, производными характеристиками. Поскольку в простом трубопроводе расход жидкости транзитный, то средняя скорость движения жидкости в трубопроводе постоянна. Для установившегося движения жидкости по трубопроводу средняя скорость движения жидкости определяется по формуле Шези: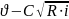 , где:

- скоростной коэффициент Шези,

гидравлический радиус сечения, для круглого сечения при полном заполнении жидкостью,

- гидравлический уклон.

Полагая, что весь имеющийся напор на головных сооружениях (в начале) трубопровода тратится на преодоление сил трения в трубопроводе (в простом трубопроводе это потери напора по длине hdt, уравнение движения жидкости (Бернулли) примет вид:

Расход жидкости в трубопроводе:

Обозначив: , получим основное уравнение простого трубопровода: где: К - модуль расхода - расход жидкости в русле заданного сечения при гидравлическом уклоне равном единице. Другой и более известный вид основного уравнения простого трубопровода получим, решив уравнение относительно напора:

Величину называют удельным сопротивлением трубопровода, - его

полным сопротивлением

График уравнения простого трубопровода H = f (Q)носит название его гидравлической характеристики.

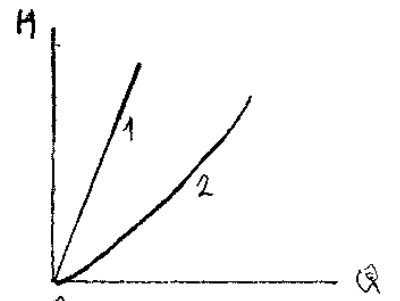
Вид гидравлической характеристики зависит от режима движения жидкости в трубопроводе: при ламинарном движении жидкости гидравлическая характеристика трубопровода - прямая линия, проходящая через начало координат (1). При турбулентном режиме гидравлическая характеристика - парабола (2).Если на трубопроводе собранном из труб одинакового диаметра имеются местные сопротивления, то такой трубопровод можно привести к простому трубопроводу эквивалентной длины