21. Потери напора в местных сопротивлениях

Как уже указывалось, помимо потерь напора по длине потока могут

возникать и так называемые местные потери напора. Причиной послед-

них, например, в трубопроводах, являются разного рода конструктивные

вставки (вход и выход трубы из резервуара, тройники, колена, сужения и

расширения трубопровода, задвижки, вентили и др.), необходимость ко-

торых вызывается условиями монтажа и эксплуатации трубопровода.

Местные сопротивления вызывают изменение скорости движения жидко-

сти по величине, направлению или величине и направлению одновременно.

В практических расчетах местные потери определяются по формуле

Вейсбаха, выражающей потери пропорционально скоростному напору:

где v – средняя скорость движения жидкости в сечении потока за мест-

ным сопротивлением; ζ – безразмерный коэффициент, называемый коэф-

фициентом местного сопротивления. Значение ζ устанавливают как пра-

вило опытным путем.

Исследованию местных сопротивлений посвящено большое число ра-

бот, в основном экспериментальных. Установлено, что ζ зависит не толь-

ко от вида самого местного сопротивления, но и от характера режима

движения жидкости, т.е. от критерия Рейнольдса Re. Однако вопрос о ме-

стных сопротивлениях при ламинарном режиме исследован еще недоста-

точно полно. Более обстоятельно исследованы явления в местных сопро-

тивлениях при турбулентном режиме. Установлено, что в этом случае из-

менение ζ в зависимости от Re незначительны. В практических расчетах

их считают зависимым только от характера и конструктивного оформле-

ния местного сопротивления.

22. Расчет потерь на местных сопротивлениях и потерь на трение по длине трубопровода

Потери напора по длине, иначе их называют потерями напора на трение  , в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением  в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью

,

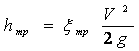где   - коэффициент сопротивления, обусловленный трением по длине.

При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине  и обратно пропорционален диаметру трубы

,

где l– коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).

Из этого выражения нетрудно видеть, что значение l - коэффициент трения участка круглой трубы, длина которого равна её диаметру.

С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси

.

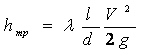Эту формулу можно применять не только для цилиндрических трубопроводов, но тогда надо выразить диаметр трубопровода d через гидравлический радиус потока

  или 

где, напомним,  Й – площадь живого сечения потока,

         З - смоченный периметр.

Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид

.

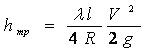Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине »не является величиной постоянной.

Для определения физического смысла коэффициента »рассмотрим объём жидкости длиной l, который равномерно движется в трубе диаметром d со скоростью V. На этот объём действуют силы давления P1 и P2, причём P1> P2, и силы трения рассматриваемого объёма о стенки трубы, которые определяются напряжением трения на стенке трубы Д0. Условием равномерного движения под действием сказанных сил будет следующее равенство:

.

Если учесть, ч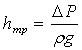то

, ^то  ,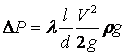

и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим:

.

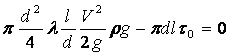Сократив последнее выражение,  получим 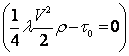  .  Выразив из него », окончательно будем иметь

.

Из полученного выражения следует, что коэффициент гидравлического трения есть величина, пропорциональная отношению напряжения трения на стенке трубы к гидродинамическому  давлению, посчитанному по средней скорости потока. Приведённые выше рассуждения и полученные в результате них формулы справедливы как для ламинарного, так и для турбулентного потоков. Однако коэффициент »не является величиной постоянной и зависит от многих факторов. Для выяснения его величины, и связанных с ним потерь энергии необходимо подробно проанализировать режимы движения жидкости.