Законы Ньютона в неинерциальных системах отсчета

Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Вообще говоря, экспериментально доказать существование ИСО невозможно, поскольку для этого необходимо наличие свободного тела (тела на которое не действуют никакие силы), а то, что тело является свободным, может быть показано лишь в ИСО. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких каксила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона:

где — сумма всех фиктивных сил в НСО.

5. Теорема о движении центра масс

Соотношение (16) очень похоже на уравнение движения материальной точки. Попробуем привести его к еще более простому виду F=ma. Для этого преобразуем левую часть, воспользовавшись свойствами операции дифференцирования (y+z) =y +z , (ay) =ay , a=const:

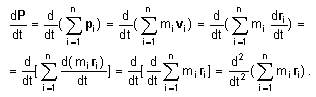(24)

Домножим и разделим (24) на массу всей системы и подставим в уравнение (16):

(25)

Выражение, стоящее в скобках, имеет размерность длины и определяет радиус-вектор некоторой точки, которая называется центром масс системы:

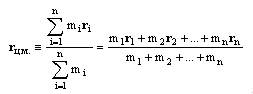(26)

В проекциях на оси координат (26) примет вид

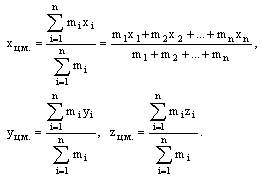(27)

Если (26) подставить в (25), то получим теорему о движении центра масс:

(28)

т.е. центр масс системы движется, как материальная точка, в которой сосредоточена вся масса системы, под действием суммы внешних сил, приложенных к системе. Теорема о движении центра масс утверждает, что какими бы сложными ни были силы взаимодействия частиц системы друг с другом и с внешними телами и как бы сложно эти частицы ни двигались, всегда можно найти точку (центр масс), движение которой описывается просто. Центр масс некая геометрическая точка, положение которой определяется распределением масс в системе и которая может не совпадать ни с одной из ее материальных частиц.

Произведение массы системы на скорость v ц.м ее центра масс, как это следует из его определения (26), равно импульсу системы:

(29)

В частности, если сумма внешних сил равна нулю, то центр масс движется равномерно и прямолинейно или покоится.

6. Формулы кинематики вращательного движения.

A=v^2/R

W=V/R – угловое ускорение

E=ax/R=w’(t) – угловое ускорение.

При вращении твердого тела, у всех его точек одинаковая угловая скорость и ускорение. Моментом силы относительно оси называется произведение силы на плечо.

Вращающее действие силы определяется именно её моментом.

Момент импульса материальной точки относительно оси ран произведению импульса на плечо.

Lz=mi Vi d

Момент силы и импульса относительно оси- это проекция векторов моментов на эту ось относительно точки, находящейся на оси.

Момент импульса твердого тела относительно неподвижной оси равен сумме моментов импульсов материальных точек, обр-их тело.

Lz=cymma mi Vi ri= cymma mi(W ri) ri= Wcymma mi ri^2

I = cymma mi ri^2 момент инерции тела относительно оси Z.

Момент инерции характеризует инерциальные свойства тела при вращении вокруг неподвижной оси.

Lz= I W –м-т импульса твердого тела.

Пример расчёта момента инерции I тонкого стержня массой m и длиной r относительно z перпенд. Стержню и проходящей через его конец.

I=lim cymma mi ri^2 = integral dm r^2

M/l= dm/dr; dm=m/l dr- масса малого отрезка стержня длинной dr

I= integral( ot 0 do e) r^2 m/l dr= m/l l^3/3= ml^2/3

Т. Штейнера.

Момент инерции тела относительно оси z равен сумме его моментов инерции относительно оси z проходящей через центр масс и произведения массы тела на квадрат расстояния между осями.

Iz=Iz’+ma^2

7. Основной закон динамики вращательного движения твердого тела формулируется так: “Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение”.

Закон сохранения момента импульса

Момент импульса тела - одна из важнейших характеристик его вращательного движения. Когда суммарный момент сил, действующих на тело, относительно данной оси вращения равен нулю , то момент импульса не изменяется:

Это и есть закон сохранения момента импульса.

Замечательной особенностью вращательного движения является свойство вращающихся тел при отсутствии взаимодействий с другими телами сохранять неизменными не только момент импульса, но и направление оси вращения в пространстве. Неизменным ориентиром для путешественников на поверхности Земли служит Полярная звезда в созвездии Большой Медведицы. Примерно на эту звезду направлена ось вращения Земли, и кажущаяся неподвижность Полярной звезды на протяжении столетий наглядно доказывает, что на протяжении этого времени направление оси вращения Земли в пространстве остается неизменным.

Неизменность направления оси вращения тел в пространстве при равенстве нулю момента внешних сил позволяет рассматривать угловую скорость вращения и момент импульса тела как векторные величины особого рода.

При сходной алгебраической форме записи закон сохранения импульса и закон сохранения момента импульса в применении к одному телу имеют существенно разный смысл. Из закона сохранения импульса следует, что тело, не взаимодействующее с другими телами, сохраняет неизменным не только свой импульс , но и из-за постоянства массы m сохраняется неизменной скорость движения .

Иначе обстоит дело в случае вращательного движения. Из закона сохранения момента импульса не следует, что при равенстве нулю момента внешних сил угловая скорость вращения тела должна оставаться неизменной, так как момент инерции тела I может изменяться внутренними силами.