17. Скорость и ускорение любой точки тела, вращающегося вокруг неподвижной оси.

    Угловой скоростью называется вектор  , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в

направлении   (   и   всегда направлены в одну сторону).

.

(2.4.1)

Если  ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси.  Пусть  v  – линейная скорость точки М. За промежуток времени dt точка М проходит

путь dr = vdt.

В то же время  dr = Rdφ  (dφ - центральный угол). Тогда, можно получить связь

линейной скорости и угловой:

.

(2.4.2)

В векторной форме  .

Вектор   ортогонален к векторам   и   и направлен в ту же сторону, что и векторное произведение  . 

Введем вектор углового ускорения   для характеристики неравномерного вращения тела:

.

(2.4.3)

Вектор   направлен в ту же сторону, что и   при ускоренном вращении  ,

а  направлен в противоположную сторону при замедленном вращении   (рис. 2.13).

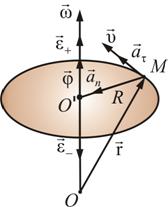  Рис. 2.13

 Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:

	aτ = Rε;	(2.4.4)

Формулы простейших случаев вращения тела вокруг неподвижной оси:

     равномерное вращение ε = 0;       ω = const;       φ = φ₀ ± ωt,

     равнопеременное вращение  .

18. Плоское движение твердого тела. Задание движения.

При плоском движении все точки тела двигаются параллельно какой либо неподвижной плоскости.

Плоским или плоскопараллель­ным движением твердого тела называ­ется такое его движение, при котором ка­ждая точка тела движется в плоско­сти, параллельной некоторой неподвижной плоскости, например движение колеса ва­гона на прямолинейном участке пути.

Рассмотрим движение плоской фи­гуры, представляющей собой сечение тела, н аходящегося в плоском движении, плоскость  , параллельной неподвижной плоскости    (рис. 2.15). При плоском движении все точки тела, лежащие на прямой  , перпендику­лярной к сечению  , т. е. к плоскости  , движутся

тождественно. Поэтому вме­сто плоского движения тела достаточно изучить движение плоской фигуры в ее плоскости.

В кинематике твердого тела изучаются три основных вопроса: задание движе­ния тела, вычисление скорости ка­кой-либо его точки и вычисление ее уско­ре­ния. Кроме этих вопросов  изучаются и другие  вопросы, представляющие на­учный и технический интерес.

Положение движущейся плоской фигуры в ее плоскости относительно не­подвижной системы осей координат    определя­ется п оложением какого-либо отрезка, жестко связанного с этой фигурой (рис. 2.16).

Положение отрезка  можно определить, зная радиус-вектор    точки    и угол  , который образует отрезок    с осью  . Точку    называют полюсом. При движении тела величины    и    будут изменяться в зависимости от времени, т. е.

  ; (2.44) . (2.45)

 

Уравнения (2.44) и (2.45) называются уравнениями плоского движения твердого тела.

Теорема. Всякое перемещение плоской фигуры в ее плоскости можно пред­ставить как совокупность двух перемещений: 1) поступательного переме­щения, зависящего от выбора полюса; 2) вращательного перемещения вокруг полюса; угол и направление поворота от выбора полюса не зависят.