6. Условия и уравнения равновесия произвольной пространственной системы сил
Для равновесия твердого тела, находящегося под действием произвольной пространственной системы сил,необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно произвольного центра О были равны нулю:
R = 0, LO = 0.
Вытекающие отсюда аналитические условия равновесия (уравнения равновесия) пространственной системы сил можно сформулировать следующим образом:
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и сумма их моментов относительно этих осей были равны нулю:
Fix =
0;
Fiy =
0;
Fiz =
0;
MOx(Fi) = 0; MOy(Fi) = 0; MOz(Fi) = 0.
Если на тело кроме сил действуют пары сил, заданные их векторными моментами Mk, то при этом вид первых трех уравнений равновесия не изменится (сумма проекций сил пары на любую ось равна нулю), а в последние три уравнения добавляются суммы проекций векторов Mk на координатные оси:
MOx(Fi) + Mkx = 0; MOy(Fi) + Mky = 0; MOz(Fi) + Mkz = 0.
7. Условия и уравнения равновесия плоской системы сил. Уравнение Вариньона о моменте равнодействующей. Изменение главного момента и главного вектора при перемене центра приведения.
Плоская система сил – система сил, расположенных в одной плоскости. Система сил приводится к одной силе – главному вектору и к паре сил, момент которой равен главному моменту. Момент пары сил направлен перпендикулярно к плоскости, в которой лежат силы. В плоских системах нет необходимости использовать векторное представление момента. Теорема Вариньона – если плоская система сил приводится к равнодействующей, то ее момент относительно какой-либо точки равен алгебраической (т.е. с учетом знака) сумме моментов всех сил относит. той же точки.
Условия равновесия пл. сист. сил:
векторное:
.
аналитич:
,
или
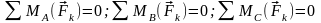где
А,В,С – точки, не лежащие на одной
прямой, или , ось "х" не перпендикулярна
отрезку АВ.
Причем вне зависимости от выбора центра приведения система сил будет приводится к одной и той же паре сил с моментом Lo. Т.к.главный вектор не зависит от выбора центра приведения.
8. Центр параллельных сил
Центр параллельных сил
Рассмотрим систему параллельных сил {F1, F2, ..., Fn}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок 1.5, а). Эта точка называется центром параллельных сил. Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).
Рисунок 1.5.Для определения координат центра параллельных сил воспользуемся этой теоремой. Относительно оси x Mx(R) = ΣMx(Fk), - yCR = ΣykFk и yC = ΣykFk /ΣFk. Mx(R) = ΣMx(Fk), - yCR = ΣykFk и yC = ΣykFk /ΣFk. Относительно оси y My(R) = ΣMy(Fk), - xCR = ΣxkFk и xC = ΣxkFk /ΣFk. My(R) = ΣMy(Fk), - xCR = ΣxkFk и xC = ΣxkFk /ΣFk. Чтобы определить координату zC, повернем все силы на 90° так, чтобы они стали параллельны оси y (рисунок 1.5, б). Тогда Mz(R) = ΣMz(Fk), - zCR = ΣzkFk и zC = ΣzkFk /ΣFk.
Mz(R) = ΣMz(Fk), - zCR = ΣzkFk и zC = ΣzkFk /ΣFk Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид rC = ΣrkFk /ΣFk.
rC = ΣrkFk /ΣFk.
Свойства центра параллельных сил: 1 Сумма моментов всех сил Fk относительно точки C равна нулю ΣMC(Fk) = 0. 2 Если все силы повернуть на некоторый угол α, не меняя точек приложения сил, то центр новой системы параллельных сил будет той же точкой C. |
