42. Механическая система. Силы внешние и внутренние. Их свойства.

Масса материальной системы. Центр масс

Масса

43. Дифференциальные уравнения движения механической системы.

Теорема о движении центра масс системы. Закон сохранения центра масс.

Количество движения механической системы. Теорема об изменении количества движения системы в дифференциальной и в конечной форме. Закон сохранения

Количества движения.

Количество движения механической системы.

44. Главный момент количества движения или кинетический момент механической системы относительно центра и оси. Кинетический момент

Вращающегося тела относительно оси вращения. Теорема об изменении

Кинетического момента системы. Закон сохранения кинетического момента.

Дифференциальные уравнения вращательного движения твердого тела.

Кинетический момент

Вращающегося тела относительно оси вращения.

Дифференциальные уравнения вращательного движения твердого тела.

45. Кинетическая энергия механической системы и твердого тела.

Вычисление кинетической энергии твердого тела в различных случаях

Его движения. Работа и мощность сил, приложенных к твердому телу,

При его вращении вокруг неподвижной оси. Теорема об изменении кинетической энергии материальной механической системы

В дифференциальной и в конечной форме.

Кинетическая энергия механической системы и твердого тела.

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек.

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

 — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы  . Учитывая, что  , Получим:

Если система замкнута, то есть  , то  , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

где:

 — масса тела

 — скорость центра масс тела

 — момент инерции тела

 — угловая скорость тела.

Работа и мощность сил, приложенных к твердому телу,

При его вращении вокруг неподвижной оси.

Работа сил, приложенных к вращающемуся телу. Элементарная работа приложенной к телу силы F (рис.49) будет равна

,

так как  , где  - угол поворота тела.

Но, как легко видеть,  . Будем называть величину   вращающим моментом. Тогда получим:  .

Следовательно, в рассматриваемом случае элементарная работа равна произведению вращающего момента на элементарный угол поворота. Формула справедлива и при действии нескольких сил, если считать  .

Р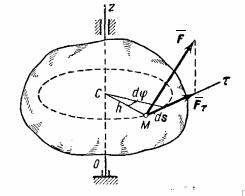 ис.49.При повороте на конечный угол   работа будет равна

,

а в случае постоянного момента 

.

Если на тело действует пара сил, лежащая в плоскости, перпендикулярной к оси Оz, то Мz будет, очевидно, означать момент этой пары.

Укажем еще, как в данном случае определяется мощность

.

Следовательно, при действии сил на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела. При той же самой мощ­ности вращающий момент будет тем больше, чем меньше угловая скорость.

Вычисление кинетической энергии твердого тела в различных случаях

Его движения.

. Теорема об изменении кинетической энергии материальной механической системы

В дифференциальной и в конечной форме.

Разделяя силы, действующие на точки системы, на внешние и внутренние, запишем для каждой точки системы теорему об изменении кинетической энергии в интегральной форме:

где A_i^e - работа внешних сил системы, приложенных к точке системы с номером i, а A_iⁱ - работа внутренних сил системы, приложенных к той же точке. Складывая между собой правые и левые части этих равенств, имеем

Сумму кинетических энергий всех точек системы обозначим T и назовем кинетической энергией системы, ту же сумму в начальном положении точек системы обозначим T₀ и назовем кинетической энергией системы в ее начальном положении, сумму работ внешних сил обозначим A^e и назовем работой внешних сил системы, сумму работ внутренних сил обозначим Aⁱ и назовем работой внутренних сил системы.

Подставляя введенные обозначения в последнее выражение, получим математическую запись теоремы об изменении кинетической энергии системы материальных точек в интегральной форме:

T - T0 = Ae + Ai

(22)

то есть: изменение кинетической энергии системы при ее переходе из начального положение в текущее (или конечное) положение равно работе внешних и внутренних сил системы, совершенной при этом переходе.

Дифференцируя (22) по времени, учитывая, что кинетическая энергия системы в начальном положении - величина постоянная, имеем dT / dt = dA^e / dt + dAⁱ / dt. Откуда, зная что производная от работы является мощностью, получаем

dT / dt = Ne + Ni

(23)

Уравнение (23) представляет собой математическую запись теоремы об изменении кинетической энергии системы материальных точек в дифференциальной форме: производная по времени от кинетической энергии системы равна мощности внутренних и внешних сил системы.

Как показывают формулы (22) и (23), в отличие от предыдущих общих теорем динамики, в теорему об изменении кинетической энергии системы входят внутренние силы. То есть непосредственно за счет внутренних сил нельзя изменить ни количество движения системы, ни ее момент количеств движения, но можно изменить ее кинетическую энергию.