- •Тема 4. Элементы векторной алгебры (12 часов, 6 лекций)
- •1. Понятие геометрического вектора, его характеристики. Виды векторов
- •2. Линейные операции над векторами в геометрической форме, их свойства
- •1. Сложение.
- •2. Вычитание.
- •3. Умножение вектора на число.
- •Лекция 2
- •3. Проекция вектора на вектор (ось), ее свойства. Направляющие косинусы вектора
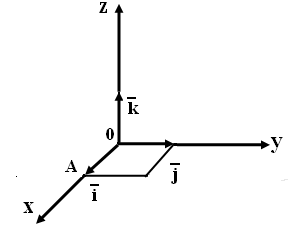
- •4. Координаты вектора (в базисе), разложение вектора по базису. Линейные операции над векторами в координатной форме
- •Лекция 4
- •6. Скалярное произведение векторов: определение, свойства, вычисление
- •Лекция 5
- •7. Векторное произведение векторов: определение, свойства, вычисление.
- •Векторное произведение в декартовой системе координат
- •Приложения векторного произведения
- •1. Вычисление площадей.
- •Лекция 6
- •8. Смешанное произведение векторов: определение, свойства, вычисление
- •Смешанное произведение в декартовой системе координат
Лекция 4
6. Скалярное произведение векторов: определение, свойства, вычисление
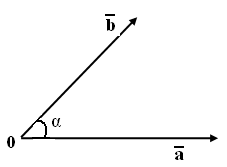
Определение 1. Углом между векторами и называется наименьший угол между этими векторами, отнесенными к общему началу.
|
Определение 2. Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
![]() (1)
(1)
Обозначения
![]() или
или
![]() .
.
![]()
![]()
Свойства скалярного произведения.
1). Коммутативность:
![]() ,
следует из определения.
,
следует из определения.
2).
![]() .
.
Доказательство.
![]() .
.
3).
![]()
Доказательство.
![]()
![]() .
.
4).
![]()
Доказательство.
![]() .
.
Из этого свойства
следует, что
![]() ,
,
![]() .
.
![]()
5). Для того, чтобы
векторы были перпендикулярны
![]() ,
необходимо и достаточно, чтобы их
скалярное произведение было равно нулю
,
необходимо и достаточно, чтобы их
скалярное произведение было равно нулю
![]() .
.
Доказательство.
а) Пусть векторы
перпендикулярны и
![]() ,
тогда
,
тогда
![]() ,следовательно,
,следовательно,
![]() и
.
и
.
б) Пусть
,
тогда
,
следовательно,
![]() .
.
6).
![]() - острый ;
- острый ;
![]() - тупой.
- тупой.
7.Для базисных ортов имеют место следующие соотношение
![]()
Скалярное произведение векторов в декартовой системе координат
Пусть даны два
вектора
![]() ,
найдем их скалярное произведение
,
найдем их скалярное произведение
![]()
![]()
воспользуемся свойством 7, получим формулу
![]() (2)
(2)
Приложения скалярного произведения
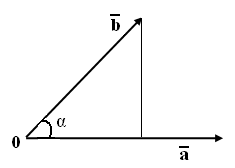
1.Вычисление проекции
![]() (3)
(3)
2.Вычисление косинуса угла между векторами
![]() (4)
(4)
3.Условие перпендикулярности векторов
![]()
Пример. Даны
векторы
![]() и
и
![]() .
Найти косинус угла между векторами.
.
Найти косинус угла между векторами.
Решение. Воспользуемся формулой (2.19) : вычисляем
![]()
![]() ,
,
![]() ,
,
Получаем
![]() .
.
Лекция 5
7. Векторное произведение векторов: определение, свойства, вычисление.
Даны три вектора с общим началом и не лежащие в одной плоскости.
Определение 1. Тройка векторов называется правой (левой), если кратчайший поворот от к виден из конца вектора происходящим против (по) часовой стрелки.
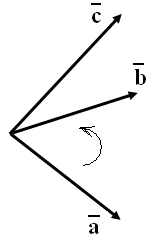
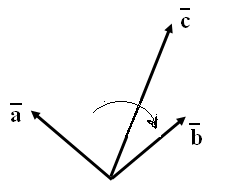
Если в тройке
поменять местами какие-то два вектора,
а третий оставить на своем месте, то
тройка изменит свою “ориентацию”.
Например, если
- правая тройка, то
![]() -
левая тройка. При циклической перестановке
векторов в тройке “ориентация” тройки
не меняется. Например, если
-
правая тройка, то
-
левая тройка. При циклической перестановке
векторов в тройке “ориентация” тройки
не меняется. Например, если
-
правая тройка, то
![]() -
тоже правая тройка.
-
тоже правая тройка.
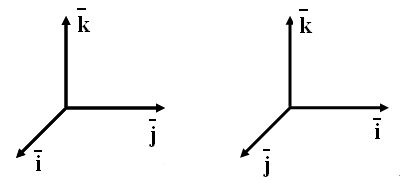
Смысл декартовой
тройки
![]() должен
соответствовать выбранному правилу.
должен
соответствовать выбранному правилу.
Определение 2. Векторным произведением двух векторов и называется вектор , удовлетворяющий следующим свойствам:
он перпендикулярен векторам и , то есть перпендикулярен плоскости векторов и ;
длина этого вектора равна площади параллелограмма, построенного на векторах и , то есть
 ;
;тройка - правая.
Обозначения
![]() или
или
![]() .
.
Свойства векторного произведения
1) Антикоммутативность:
![]()
Доказательство.
Пусть
,
построим вектор
![]() .
.
![]() ,
то есть
,
то есть

длины векторов
и
![]() равны , но чтобы тройка векторов
равны , но чтобы тройка векторов
![]() была правой, вектор
должен быть противоположен вектору
,
следовательно,
была правой, вектор
должен быть противоположен вектору
,
следовательно,
![]() .
.
2). Если в векторном
произведении изменить знак одного из
множителей, то произведение тоже изменит
знак:
![]() .
.
Доказательство.

3).
![]()
Доказательство.
а) Для
![]() очевидно;
очевидно;
б) для
![]() :
если длина одной из сторон параллелограмма
изменяется в
раз, то площадь параллелограмма тоже
изменится в
раз;
:
если длина одной из сторон параллелограмма
изменяется в
раз, то площадь параллелограмма тоже
изменится в
раз;
в) для
![]() :
:
![]() .
.
4).
![]() .
.

Доказательство.
Возьмем единичный вектор
![]() ,
перпендикулярный плоскости
,
перпендикулярный плоскости
![]() ,
,
![]() .
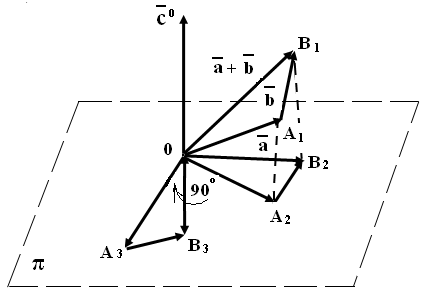
Спроектируем вектор
на плоскость
,
получим вектор
.
Спроектируем вектор
на плоскость
,
получим вектор
![]() ,
повернем его в плоскости
вокруг точки
,
повернем его в плоскости
вокруг точки
![]() по часовой стрелке на
по часовой стрелке на
![]() :
а)
:
а)
![]() ;
;
б)
![]() (
так как
(
так как
![]() ,
,
![]() (
так как
(
так как
![]() ,
а
-
проекция
тогда по теореме о трех перпендикулярах
выполняется этот факт);
,
а
-
проекция
тогда по теореме о трех перпендикулярах
выполняется этот факт);
в)
![]() -
правая тройка, следовательно,
-
правая тройка, следовательно,
![]() .
.
Вектор
![]() .
В
.
В
![]()
![]() .
Спроектируем данный треугольник на
плоскость
, получим
.
Спроектируем данный треугольник на
плоскость
, получим
![]() ,
повернем его в плоскости
по часовой стрелке на
,
,
повернем его в плоскости
по часовой стрелке на
,
получим
![]() .
.
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
![]() ,
тогда
,
тогда
![]() ,
следовательно,
,
следовательно,
.
5).
![]() .
.
6). Для того, чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было равно нулю.
Доказательство.
а) Пусть векторы
и
коллинеарны,
следовательно,
![]() или
или
![]() ,
тогда
,
тогда
![]() и
и
![]() ,
нулевую длину имеет только нулевой
вектор, то есть
,
нулевую длину имеет только нулевой
вектор, то есть
![]() ;
;
б) Пусть
![]() ,
тогда
,
но
,
тогда
,
но
![]() ,
следовательно,
,
следовательно,
, а это значит, что и коллинеарны.
7).
![]() .
.
8). Векторные произведения базисных ортов можно представить в виде таблицы:
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
Пояснение: векторное
произведение
![]() - это вектор, перпендикулярный векторам
и
,
длина которого равна площади квадрата,
построенного на векторах
и
,
то есть равна 1 , а тройка векторов
-
правая тройка, отсюда следует, что
- это вектор, перпендикулярный векторам
и
,
длина которого равна площади квадрата,
построенного на векторах
и
,
то есть равна 1 , а тройка векторов
-
правая тройка, отсюда следует, что
![]() .
Остальные произведения можно получить,
используя свойства векторного
произведения.
.
Остальные произведения можно получить,
используя свойства векторного
произведения.