МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Инженерно-экономический факультет

Кафедра эконометрики и математического моделирования (ЭиММ)

ЛЕКЦИИ ПО ДИСЦИПЛИНЕ

«Линейная алгебра»

для направления 080100 «Экономика»

Рязань 2012

Тема 4. Элементы векторной алгебры (12 часов, 6 лекций)

Лекция 1

1. Понятие геометрического вектора, его характеристики. Виды векторов

В физике и других науках встречаются два типа величин: скалярные и векторные. Скалярные величины характеризуются численным значением в выбранной системе единиц. Это масса, температура, объем. Векторные величины характеризуются численным значением и направлением. Это сила, скорость, ускорение.

Определение 1. Геометрический вектор - это направленный отрезок.

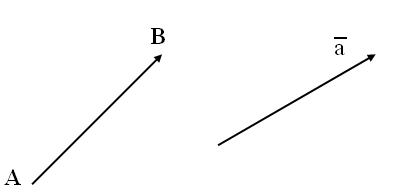
Определение 2. Модуль вектора, или длина вектора – это расстояние между нач алом концом вектора. Обозначения , .

Определение 3. Два вектора называются равными, если они имеют одинаковую длину и одинаково направлены (параллельны и направлены в одну сторону).

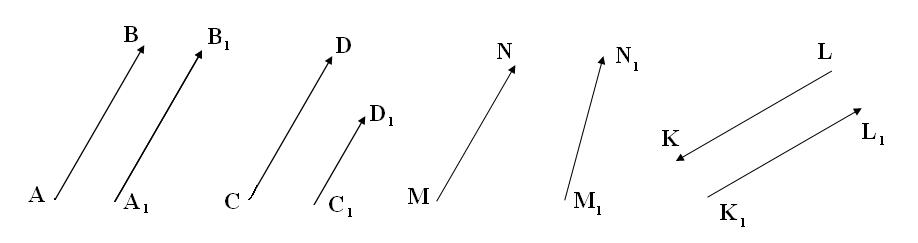
Рис. 1

На рис. 1 векторы и равные, векторы и имеют разную длину, а векторы и , и имеют разные направления.

Определение 4. Два вектора называются коллинеарными, если они лежат на одной прямой или параллельны одной прямой ( ) .

Определение 5. Три вектора называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости.

Коллениарные -если они лежат на одной прямой или лежат на двух разных параллельных прямых.

Ортогональные – если лежат на двух взаимно перпендикулярных прямых.

2. Линейные операции над векторами в геометрической форме, их свойства

1. Сложение.

а) правило параллелограмма: если векторы имеют общее начало, то сумма векторов – это вектор, являющийся диагональю параллелограмма, построенного на данных векторах.

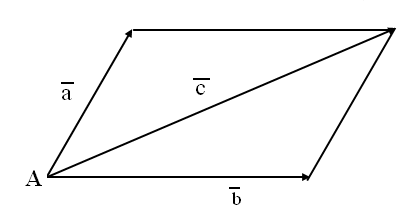
Из рисунка видно, что .

Рис. 1

б) правило треугольника: если векторы расположены последовательно, то есть конец первого является началом второго, то сумма векторов – это вектор, начало которого является началом первого, конец – это конец второго.

Рис. 2

Используя это правило, легко доказать, что

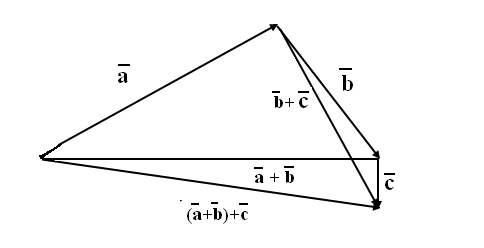
в) правило многоугольника: это обобщение правила треугольника, используется при последовательном расположении нескольких векторов, сумма нескольких последовательных векторов – это вектор, начало которого – это начало первого, а конец – это конец последнего.

Определение 1. Вектор, начало и конец которого совпадают, называется нулевым, его длина равна нулю, направление любое.

Определение 2. Если поменять начало и конец вектора местами, то получится вектор, противоположный данному.