25.Многомерные св.
Если знач.СВ определяется парами чисел (х;у), то такая СВ наз-ся двумерной, а если (x;y;z), то- трехмерной и т.д.
Многомерные СВ бывают: дискретные и непрерывные. X и Y. Двумерную СВ можно трактовать как случайную точку на плоскости или случайный вектор.
Простой формой ЗР ДСВ явл-ся табл.распр-я.
26.Ф-ция распр.двумерной СВ и ее св-ва.
Опр.1: Функцией распределения двухмерной СВ (X;Y) наз-ся F(x;y)=P(X<x, Y<y).
Свойства:
1.
2. F(x,y) есть неубывающая функция по каждой переменной
X1<x2 => F(x1,y)<=F(x2,y)
Y1<y2 => F(x, y1)<=F(x, y2)
3.
4.
Плотностью вероятности непрерывной двухмерной СВ (Х, У) называется смешанная частная производная 2го порядка ее функции распределения
P(x,y)=Fx,y(x,y)
27.Условные зр. Зависимые и незав.Св.
Опр.1: Условным ЗР составляющей Х наз-ся ее ЗР, найденный при усл.,что сост.Y прин-ла опр.знач. Yj (Y=yj)
A: Y=yj ;
B: X=xj ;
AB=(X=xj, Y=yj)
P(AB)=pij ; P(A)=qj ; P(B)=pi
Pj(xi)=PY=yj(X=xi)=Pij /qij (1)
i=1,…,n
(1) задает условный закон распр. сост.Х
Pi(yj)=PX=xi(Y=yj)= Pij / pi (2)
(2) задает усл.зак.распр. сост У
Опр.2: Две СВ Х и У наз-ся независимыми, если ЗР одной из них не зависит от того, какое знач. приняла др. pij=pi qj ; pj(xi)=pi
Если СВ Х и У независимыми, то ф-ция распр-я двухмерной СВ F(x,y), то
F(x,y)=F1(x) F2(y), где F1(x) и F2(y)- ф-ции распр.сост-х Х и У. Для непрер. СВ в случ.незав-ти будет вып-ся рав-во p(x,y)=p1(x) p2(y).
28.Числовые хар-ки с-мы св. Корреляционный момент и коэффициент корреляции.
Опр.1: Корреляционным моментом ДвСВ (Х,У) наз-ся матем.ож.поизведения отклонения СВ от своих матем.ож.
(Х,У)=Кху=М[(Х-М(Х))(У-М(У))]
Св-ва: 1.Кху=Кух
2.Кхх=М [ (X-M(X))2 ]=D(X)
3.Если СВ Х и У независимы, то их кор.мом.=0. Обратное утверждение в общем случае не верно. Если Кху=0, то СВ Х и У наз-ся некоррелированными
4.Кху= М(ХУ)-М(Х)М(У)
М(ХУ)=М(Х)М(У)+Кху
5.lКхуl
Коррел.мом.хар-ет как степень зав-ти СВ Х и У, так и рассеяние случ.точки (Х;У) относительно точки (М(Х);М(У)). Данная величина явл-ся размерной.
Опр.2: Коэф.
корреляции
СВ Х и У наз-ся величина rxy
= Kxy
/
.
Св-ва: 1. rxy=ryx
2.rxx=1
3. lrxy l
4. Если СВ Х и У независ.,то коэф.кор=0: rxy =0.
5. Если коэф.кор.=1, то м/у Х и У сущ-ет линейная функциональная зависимость.
29.Неравенство Маркова. Неравенство Чебышева.
Т1: Нер-во Маркова.
Если СВ Х принимает только неотр.знач. и имеет мат.ож., то для любого полож.числа А имеет место нер-во :
Т2: Нер-во Чебышева.
Если Св Х имеет мат.ож и дисперсию, то для любого полож.числа Е справ-во нер-во:
Следствие 1:
Следствие 2: Для СВ Х, имеющ.биномиальный ЗР с М(Х)=np, D(X)=npq, то
30.Теорема Чебышева.
Т1: Т.Чебышева.
Если дисперсии n незав.СВ х1,х2,…,хn с М(Х1)=а1, М(Х2)=а2,…, М(Хn)=an огранич. Одной и той же постоянной, то для любого полож.числа Е имеет место рав-во :
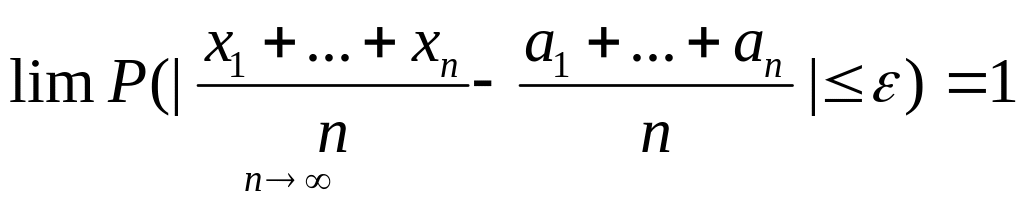
Данное рав-во означ.,что ср.арифм. СВ сх-ся по вер-ти ср.ар. их матем.ож.
Смысл т.Чебышева при большом n практич.достоверно, что ср.арифм. n СВ явл-ся вел.случ., сколь угодно мало отл-ся от ср.ариф. их мат.ож, вел.постоянной.
Следствие: Если дисперсии n СВ х1,…,хn с мат.ож а1,…,аn огранич. Одной и той же постоянной С, т.е. D(Xi)<=C, i=1,…,n, nо для любого Е>0 имеет место нер-во:
