§5. Разложение силы на составляющие

Для решения многих задач бывает необходимо рассмотреть обратную ситуацию – найти несколько сил, которые своим совместным действием могли бы заменить одну данную силу. Такие силы называются составляющими, а сама операция называется разложением сил на составляющие. В качестве иллюстрации рассмотрим частные случаи разложения силы на две составляющие, когда и сила, и её составляющие лежат в одной плоскости.

Задачу разложения силы на две составляющие можно решить, пользуясь правилом параллелограмма, причём исходная сила рассматривается как его диагональ. Но параллелограммов с одинаковой заданной диагональю можно построить сколь угодно много (рис.8).

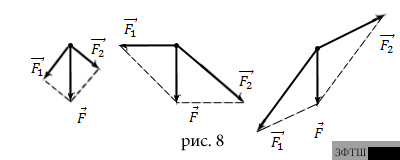
Для того, чтобы задача стала определённой и решалась однозначно, необходимо кроме заданной силы указать одно из следующих условий:

• известны направления обеих составляющих сил;

• известны величина одной из составляющих и её направление.

Пример 7. Сила   приложена в точке В кронштейна и направлена вертикально вниз (рис.9а). Найдите составляющие этой силы по направлениям стержней кронштейна. Необходимые данные указаны на рисунке.

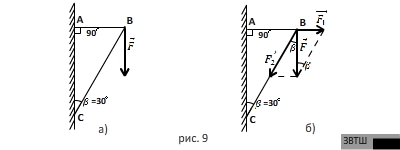
РЕШЕНИЕ. Пусть стержни прикреплены к стене в точках   и  . Разложение силы   на составляющие вдоль направлений   и   представлено на рис.9б. Откуда видно, что  ;  .

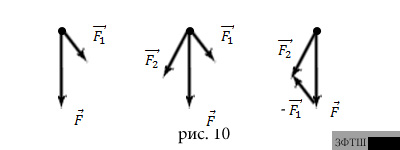
Пример 8. Дана сила   и её составляющая сила  (рис.10а). Найдите вторую составляющую силы  .

РЕШЕНИЕ. Задача сводится к построению параллелограмма по диагонали и одной из сторон, известному из планиметрии. На рис.10б построен такой параллелограмм и указана искомая составляющая   силы  Второй способ решения: прибавить к силе   силу, равную  (рис.10в). В результате получим искомую силу  .

В начало

§6. Второй закон Ньютона

Второй закон Ньютона утверждает, что в инерциальных системах отсчёта ускорение   тела прямо пропорционально равнодействующей   всех приложенных к телу сил и обратно пропорционально массе тела: 

В более удобном виде можно записать:  (1)

Видим, что векторы   и   коллинеарные и, так как масса тела – величина положительная, то направления этих векторов одинаковы. В свою очередь направления скорости тела и перемещения тела могут не совпадать с направлением вектора  .

Учитывая, что по определению   (см. выше), выражение (1) можно написать в виде:  (1.1) после чего его можно переписать для проекций ускорения и сил на оси выбранной системы координат. Если все силы, действующие на тело, лежат в одной плоскости, то можно ограничиться двумя координатными осями   и  . Тогда получим систему двух скалярных уравнений 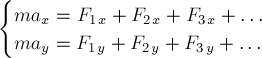 (1.2) равносильную одному векторному уравнению (1.1).

Пример 9. Тело, массой   движется с ускорением  . Выберите правильное утверждение.

1. Равнодействующая всех приложенных к телу сил равна 10Н.

2. Равнодействующая всех приложенных к телу сил равна нулю.

3. Равнодействующая всех приложенных к телу сил равна 1Н.

ОТВЕТ. Верно утверждение 3).

Действительно, в соответствии с выражением (1) модуль равнодействующей равен произведению массы тела на модуль ускорения. В нашем случае это произведение равно  .

Пример 10. Под действием силы   тело движется прямолинейно вдоль оси   так, что его координата изменяется со временем по закону  . Какова масса тела?

РЕШЕНИЕ. Видим, что зависимость   соответствует случаю равноускоренного движения. Следовательно, коэффициент при   равен половине проекции ускорения тела на ось  . Таким образом, в нашем случае  ,   и, значит,  .

Пример 11. На тело массой   действуют сила   под углом   к оси   и сила   под углом   к оси   (рис.11а). Найдите проекции ускорения тела на оси   и   и само ускорение тела.

РЕШЕНИЕ. В данном случае система уравнений (1.2) имеет вид (рис.11б):  Отсюда получаем 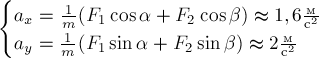 Модуль ускорения равен  . Направление ускорения тела определим с помощью угла   между вектором ускорения и осью   (рис.11в). Угол   таков, что  .

В начало