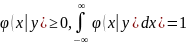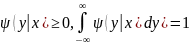23. Плотность совместного распределения вероятностей двумерной случайной величины и ее свойства. Вероятность попадания точки в произвольную область.

Плотностью совместного распределения вероятностей 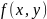двумерной непрерывной случайной величины называют вторую смешанную частную производную от функции распределения: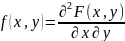

Обратное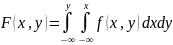

Вероятность попадания точки в произвольную область.

и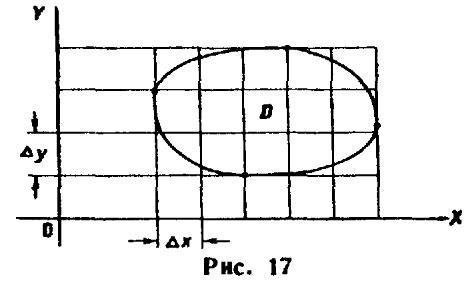 з этого можно получить

Получим:

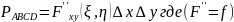
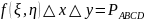
Пусть в плоскости задана произвольная область D.

Разобьем область D на n элементарных областей

Вероятность попадания в область D приближенно (сумма элементарных областей приближенно равна области D!) равна сумме вероятностей попаданий точки в элементарные области:

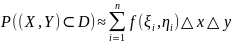
Переходим к переделу при 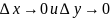получим:

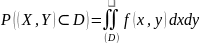
свойства плотности:

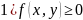2)

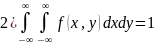
24. Нахождения частных законов распределения для дискретной и непрерывной случайной величины.

Зная плотность совместного распределения f(x, у), можно найти функцию распределения F(х, у) по формуле

F(x,y) =

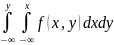
Дискретная СВ, т.е. набор конкретных значений.

Распределение задано матрицей:

x\y	Y1	…	Ym
X1	P11
…		…
Xn			Pnm

Частные законы распределения:

X	X1	…	Xn
Px	Px1	…	Pxn

Pxi = Pi1+…+Pim (т. е. cуммируем все значения в строке, соответствующей Xi)

Аналогично находится закон распределения Y – суммируем значения в столбце, соотв. Yi.

====== =============== ======================

Непрерывная СВ.

Задана плотностью распределения f(x,y)

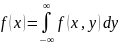
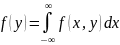
25. Условные законы распределения компонент дискретных и непрерывных двумерных случайных векторов.

Для дискретных величин:

Известно, что если события А я В зависимы, то условная вероятность события В отличается от его безусловной вероятности. В этом случае

P_A(B) = P(AB) / P(A) (*)

Аналогичное положение имеет место и для случайных величин. Для того чтобы охарактеризовать зависимость между составляющими двумерной случайной величины, введем понятие условного распределения.

понятие условного распределения.

Рассмотрим дискретную двумерную случайную величину (X, У). Пусть возможные значения составляющих таковы: x_1, x₂, …, x_n; y₁, y_2, …, y_n

Допустим, что в результате испытания величина У приняла значение Y = у₁ при этом X примет одно из своих возможных значений: x₁ или x₂,…, или х_n. Обозначим условную вероятность того, что X примет, например, значение x₁при условии, что Y = у₁, через p(x₁|у₁).Эта вероятность, вообще говоря, не будет равна безусловной вероятности р(х₁).

В общем случае условные вероятности составляющей будем обозначать так:

p(x_i|у_j). (i = 1, 2, .... n; j =1, 2, ..., m).

Условным распределением составляющей X при У — y_j называют совокупность условных вероятностей p(x₁|у_j), p(x₂|у_j), …, p(x_n|у_j)вычисленных в предположении, что событие Y = Уj (j имеет одно и то же значение при всех значениях X) уже наступило. Аналогично определяется условное распределение составляющей Y.

Зная закон распределения двумерной дискретной случайной величины, можно, пользуясь формулой (*), вычислить условные законы распределения составляющих. Например, условный закон распределения X в предположении, что событие Y = yx уже произошло, может быть найден по формуле

p(x_i|у₁) = 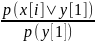(i=1, 2, .... n).

В общем случае условные законы распределения составляющей X определяются соотношением

p(x_i|у_j) = p(x_i|у_j) / p(y_j) (**)

Аналогично находят условные законы распределения

составляющей У:

p(у_j | x_i) = p(x_i|у_j) / p(x_j)

Замечание: Сумма вероятностей условного распределения равна единице. Действительно, так как при фиксированном y_j имеем

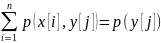, то

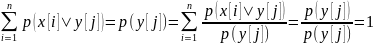
Аналогично доказывается, что при фиксированном x_i

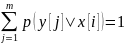
Для непрерывных величин:

Пусть (X, Y) — непрерывная двумерная случайная величина.

Условной плотностью 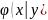распределения составляющих X при данном значении Y = y называют отношение плотности совместного распределения 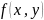системы (X, Y) к плотности распределения f₂(y) составляющей Y:

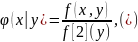
Подчеркнем, что отличие условной плотности от безусловной плотности f₁(x) состоит в том, что функция дает распределение X при условии, что составляющая Y приняла значение Y = у; функция же f₁(х) дает распределение X независимо от того, какие из возможных значений приняла составляющая Y.

Аналогично определяется условная плотность составляющей У при данном значении X = х:

ψ 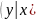= f(x,y) / f₁(x) (**)

Если известна плотность совместного распределения f(х, у), то условные плотности составляющих могут быть найдены в силу (*) и (**) (см. § 12) по формулам:

/ (***)

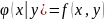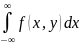ψ = / (****)

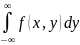Запишем формулы (*) и (**) в виде

f(x, y) = f₂(y) , f(x,y) = f₁(x) ψ

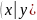
Отсюда заключаем: умножая закон распределения одной из составляющих на условный закон распределения другой составляющей, найдем закон распределения системы случайных величин.

Как и любая плотность распределения, условные плотности обладают следующими свойствами: