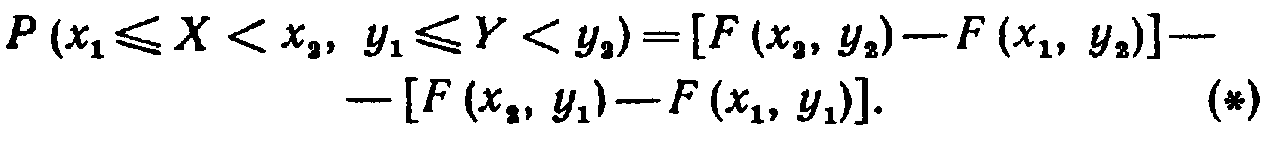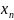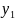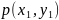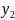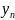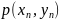- •1. Понятие случайного события. Элементарное, сложное, невозможное, достоверное события. Операции над событиями (равенство, объединение, пересечение, отрицание, разность). Примеры.
- •2. Классическое определение вероятности. Примеры.
- •3. Основные формулы комбинаторики. Примеры.
- •4. Геометрическая вероятность. Примеры.
- •Случайные величины. Дискретные случайные величины. Закон распределения дискретной случайной величины.
- •Случайная величина. Непрерывные случайные величины. Функция распределения вероятностей, плотность распределения. Определение и свойства
- •13. Числовые характеристики случайной величины. Определение математического ожидания, начальные и центральные моменты, дисперсия, среднеквадратическое отклонение, квантили случайной величины.
- •14. Распределение Пуассона и его числовые характеристики.
- •15. Равномерное распределение и его числовые характеристики.
- •17. Нормальная функция распределения. Характеристики нормального распределения. Стандартное нормальное распределение. Свойства стандартного нормального распределения.
- •18. Вероятность попадания нормально распределенной случайной величины на заданный интервал. Функция Лапласа. Связь нормальной функции распределения с функцией Лапласа. Свойства функции Лапласа.
- •19. Вычисление вероятности заданного отклонения. Правило «трех сигм».
- •20. Система двух случайных величин. Таблица распределений для дискретной системы. Частные законы распределения компонент случайного вектора.
- •21. Система двух случайных величин. Функция распределения двумерной случайной величины. Определение случайного вектора, основные свойства его функции распределения.
- •22. Вероятность попадания случайной точки в полуполосу и прямоугольник.
- •23. Плотность совместного распределения вероятностей двумерной случайной величины и ее свойства. Вероятность попадания точки в произвольную область.
- •24. Нахождения частных законов распределения для дискретной и непрерывной случайной величины.
- •25. Условные законы распределения компонент дискретных и непрерывных двумерных случайных векторов.
- •26. Свойства математического ожидания и дисперсии.
- •27. Коэффициент ковариации и его свойства. Коэффициент корреляции как мера связи случайных величин. Коэффициент корреляции
- •28. Зависимые и независимые случайные величины.
20. Система двух случайных величин. Таблица распределений для дискретной системы. Частные законы распределения компонент случайного вектора.
До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом.
Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя, ..., n числами. Такие величины называются соответственно двумерными, трехмерными, . . ., n-мерными.
(X, Y) двумерная случайная величина.
Каждую
из величин
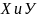 называют составляющей
(компонентой);
называют составляющей
(компонентой);
система
двух случайных величин -
величины
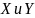 ,
рассматриваемые одновременно.
,
рассматриваемые одновременно.
Пример. Станок-автомат штампует стальные плитки. Если контролируемыми размерами являются длина X и ширина Y, то имеем двумерную случайную величину (X, Y);
Законом
распределения дискретной двумерной
случайной величины
называют перечень возможных значений
этой величины, т. е. пар чисел
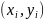 и
их вероятностей.
и
их вероятностей.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
События
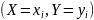 образуют
полную группу, то сумма вероятностей,
помещенных во всех клетках таблицы,
равна единице.
образуют
полную группу, то сумма вероятностей,
помещенных во всех клетках таблицы,
равна единице.
Утв. вероятность того, что X примет значение , равна сумме вероятностей «столбца »(законы распределения составляющей X)
21. Система двух случайных величин. Функция распределения двумерной случайной величины. Определение случайного вектора, основные свойства его функции распределения.
(X, Y) двумерная случайная величина.
Каждую из величин называют составляющей (компонентой);
система двух случайных величин - величины , рассматриваемые одновременно.
Функцией
распределения двумерной случайной
величины
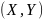 называют
функцию
называют
функцию
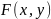 ,
определяющую для каждой пары чисел
,
определяющую для каждой пары чисел
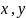 вероятность того, что
примет значение, меньшее
вероятность того, что
примет значение, меньшее
 ,
и при этом
,
и при этом
 примет значение, меньшее
примет значение, меньшее
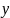 :
:

![]()
![]() Применима
графическая интерпретация на плоскости
xy
Применима
графическая интерпретация на плоскости
xy
 4
свойства функции распределения двумерной
случайной величины
4
свойства функции распределения двумерной
случайной величины
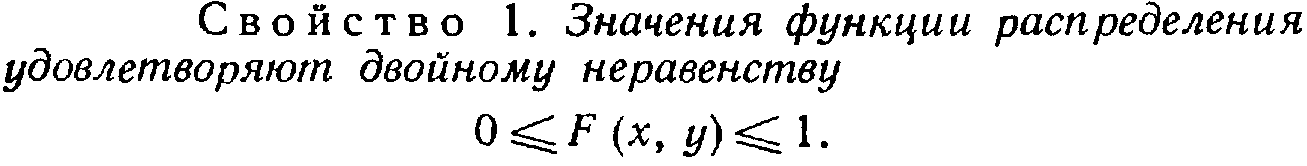
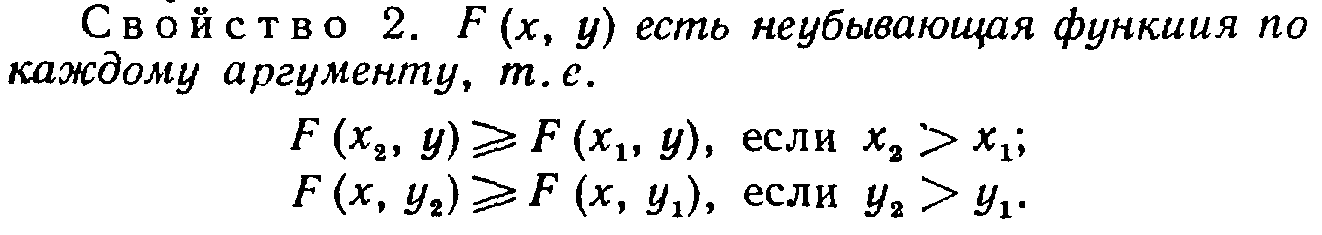
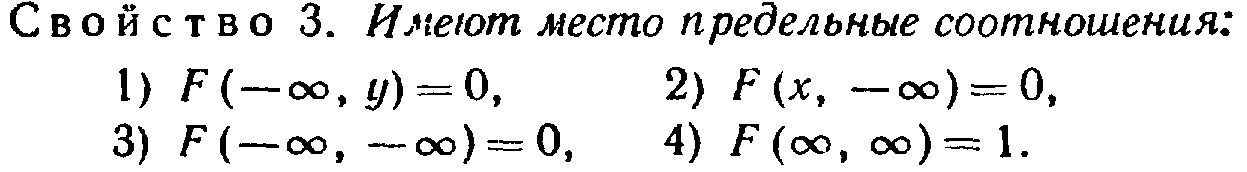
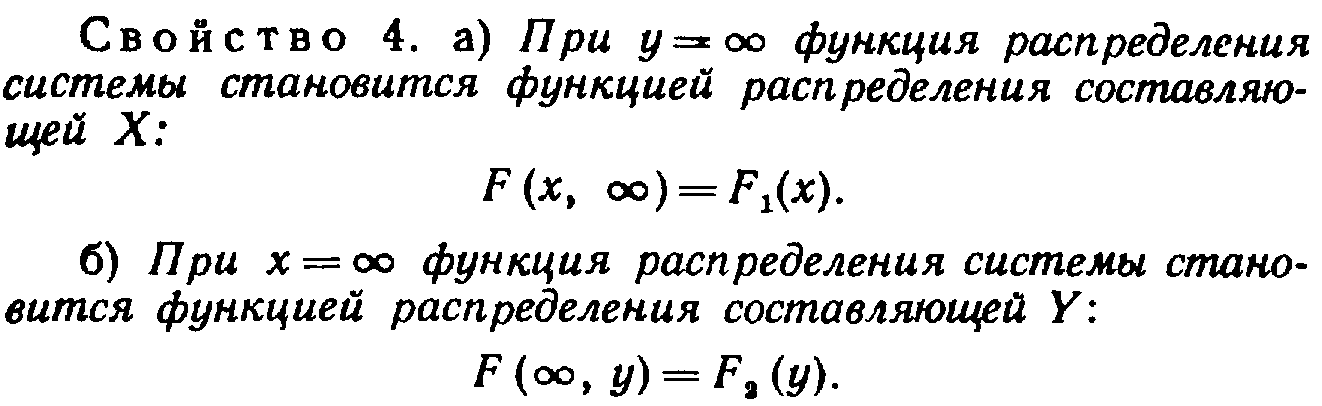
Случайный
вектор в теории
вероятностей —
вектор ![]() ,
компонентами которого служат случайные
величины
,
компонентами которого служат случайные
величины ![]() ,
совместное распределение которых
задается вероятностями
,
совместное распределение которых
задается вероятностями
![]()
где ![]() —
борелевское подмножество, которые
однозначно определяются n-мерной
функцией распределения(если про эту
хренотню промолчите вам же будет лучше)
—
борелевское подмножество, которые
однозначно определяются n-мерной
функцией распределения(если про эту
хренотню промолчите вам же будет лучше)
![]()
Абсолютно
непрерывное распределение случайного
вектора ![]() пределяется
плотностью
пределяется
плотностью ![]() :
:
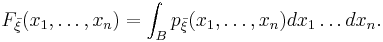
Дискретное
распределение случайного
вектора
определяется
не более, чем счётным числом
вероятностей 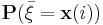 так,
что
так,
что
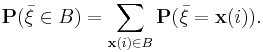
22. Вероятность попадания случайной точки в полуполосу и прямоугольник.

Вероятность попадания случайной точки
в прямоугольник
Рассмотрим прямоугольник ABCD со сторонами,
параллельными координатным осям (рис. 15). Пусть уравнения сторон таковы:
![]()
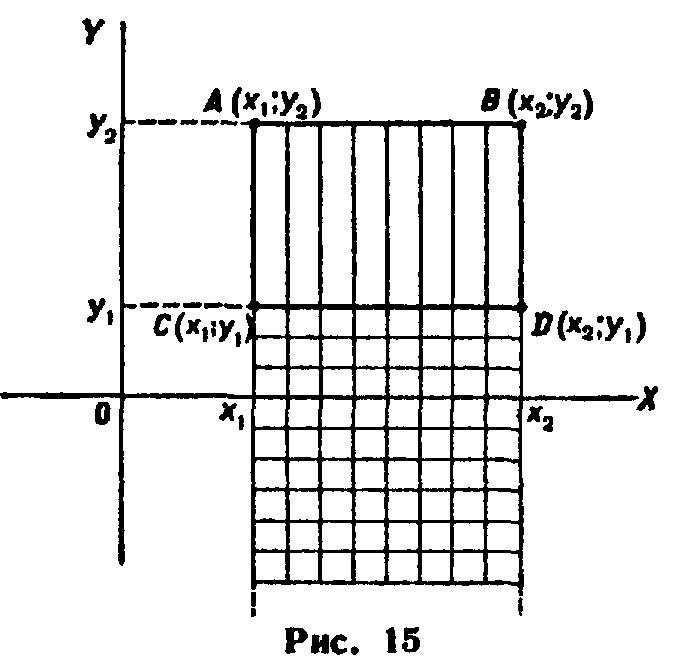
Найдем вероятность попадания случайной точки (X; У) в этот прямоугольник. Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полу полосу А В с вертикальной штриховкой
(эта
вероятность равна![]() )
)
вычесть вероятность попадания точки в полуполосу CD с горизонтальной
штриховкой
(эта
вероятность
равна
![]() ):
):