
- •1. Понятие случайного события. Элементарное, сложное, невозможное, достоверное события. Операции над событиями (равенство, объединение, пересечение, отрицание, разность). Примеры.
- •2. Классическое определение вероятности. Примеры.
- •3. Основные формулы комбинаторики. Примеры.
- •4. Геометрическая вероятность. Примеры.
- •Случайные величины. Дискретные случайные величины. Закон распределения дискретной случайной величины.
- •Случайная величина. Непрерывные случайные величины. Функция распределения вероятностей, плотность распределения. Определение и свойства
- •13. Числовые характеристики случайной величины. Определение математического ожидания, начальные и центральные моменты, дисперсия, среднеквадратическое отклонение, квантили случайной величины.
- •14. Распределение Пуассона и его числовые характеристики.
- •15. Равномерное распределение и его числовые характеристики.
- •17. Нормальная функция распределения. Характеристики нормального распределения. Стандартное нормальное распределение. Свойства стандартного нормального распределения.
- •18. Вероятность попадания нормально распределенной случайной величины на заданный интервал. Функция Лапласа. Связь нормальной функции распределения с функцией Лапласа. Свойства функции Лапласа.
- •19. Вычисление вероятности заданного отклонения. Правило «трех сигм».
- •20. Система двух случайных величин. Таблица распределений для дискретной системы. Частные законы распределения компонент случайного вектора.
- •21. Система двух случайных величин. Функция распределения двумерной случайной величины. Определение случайного вектора, основные свойства его функции распределения.
- •22. Вероятность попадания случайной точки в полуполосу и прямоугольник.
- •23. Плотность совместного распределения вероятностей двумерной случайной величины и ее свойства. Вероятность попадания точки в произвольную область.
- •24. Нахождения частных законов распределения для дискретной и непрерывной случайной величины.
- •25. Условные законы распределения компонент дискретных и непрерывных двумерных случайных векторов.
- •26. Свойства математического ожидания и дисперсии.
- •27. Коэффициент ковариации и его свойства. Коэффициент корреляции как мера связи случайных величин. Коэффициент корреляции
- •28. Зависимые и независимые случайные величины.
15. Равномерное распределение и его числовые характеристики.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
![]() то
то
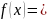
при большом желании и присутствии мазохизма можно вывести 1/b-a ручками из свойства нормировки плотности
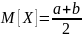
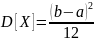
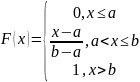 16.
Показательное
распределение и его числовые характеристики.
16.
Показательное
распределение и его числовые характеристики.
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
f(x)
=
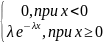
где
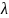 —постоянная положительная величина.
—постоянная положительная величина.
Функция распределения показательного закона
F(x)
=
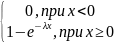
Вероятность попадания в интервал (а, Ь) непрерывной случайной величины X, распределенной по показательному закону»
P(a
< X < b) =
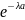 -
-
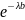
Математическое ожидание, дисперсия и среднеквадратическое отклонение показательного распределения соответственно равны:
M(X)
= =
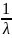 ,
D(X)
=
,
D(X)
=
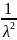 ,
,
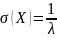
Таким образом, математическое ожидание и среднеквадратическое отклонение показательного распределения равны между собой.
17. Нормальная функция распределения. Характеристики нормального распределения. Стандартное нормальное распределение. Свойства стандартного нормального распределения.
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
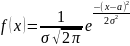
записывается
нормальное распределение в виде
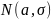 ,
где а - коэффициент
сдвига,
σ
> 0 - коэффициент
масштаба
,
где а - коэффициент
сдвига,
σ
> 0 - коэффициент
масштаба
М
(X) = а,
т. е. математическое ожидание нормального
распределения равно параметру
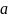 .
.
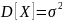
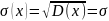 ,
т.е. Среднее квадратическое отклонение
нормального распределения равно
параметру
,
т.е. Среднее квадратическое отклонение
нормального распределения равно
параметру
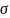 .
.
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
Свойство 1
Если
случайные величины X1 и X2 независимы
и имеют нормальное распределение с
математическими ожиданиями μ1 иμ2 и
дисперсиями ![]() и
и ![]() соответственно,
то X1 + X2 также
имеет нормальное распределение с
математическим ожиданием μ1 +
μ2 и
дисперсией
соответственно,
то X1 + X2 также
имеет нормальное распределение с
математическим ожиданием μ1 +
μ2 и
дисперсией ![]() .
.
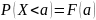
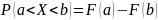
и
вроде как
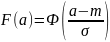
18. Вероятность попадания нормально распределенной случайной величины на заданный интервал. Функция Лапласа. Связь нормальной функции распределения с функцией Лапласа. Свойства функции Лапласа.
Уже
известно, что если случайная величина
задана плотностью распределения
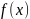 ,
то вероятность того, что
примет значение, принадлежащее интервалу
,
то вероятность того, что
примет значение, принадлежащее интервалу
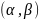 ,
такова:
,
такова:
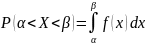
Пусть случайная величина X распределена по нормальному закону. Тогда :
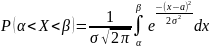
Преобразуем
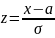 тогда имеем:
тогда имеем:
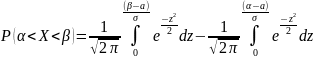
Пользуемся функ.Лапласса
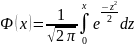
получим:
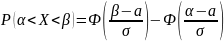
Свойства функции Лапласа:
1)
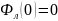
2)
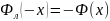
3)
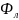 (х)
- бесконечно возрастающая
(х)
- бесконечно возрастающая
19. Вычисление вероятности заданного отклонения. Правило «трех сигм».
Требуется
вычислить вероятность того, что отклонение
нормально распределенной случайной
величины
X
по абсолютной величине меньше заданного
положительного числа
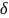 ,
т. е. требуется найти вероятность
осуществления неравенства
,
т. е. требуется найти вероятность
осуществления неравенства
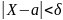
Пользуясь нормальной функцией распределения:
Получим
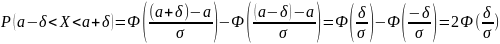
сущность правила трех сигм:
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
Преобразуем
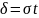
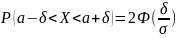
Получим
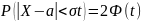
Если
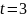 и следовательно
и следовательно
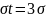 то
то
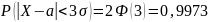
Такие события (0,0027) исходя из принципа невозможности маловероятных событий можно считать практически невозможными.
