33

1. Понятие случайного события. Элементарное, сложное, невозможное, достоверное события. Операции над событиями (равенство, объединение, пересечение, отрицание, разность). Примеры.

Вероятность – некоторое число в интервале [0;1].

Совокупность всех возможных, различных, конкретных исходов испытаний называется пространством элементарных событий.

Сложным событием называется произвольное подмножество пространства элементарных событий.(wtf????)

сложным называется событие состоящие из нескольких связанных между собой событиями

нарисовать диаграммы Эйлера-Вена для всех случаев и будет счастье

2. Классическое определение вероятности. Примеры.

определение классической вероятности

классическая веротяность предполагает что все исходы экспиримента равновероятны

СВОЙСТВА:

3. Основные формулы комбинаторики. Примеры.

Пусть множество А состоит из n различных элементов различных типов, причем K₁ элементов I-ого типа, К₂ элементов II-ого, …, K_m элементов m-ого типа. Тогда всевозможные множества из n элементов называются перестановкой с повторениями.

4. Геометрическая вероятность. Примеры.

5. Теоремы сложения вероятностей совместных и несовместных событий. Примеры.

если события совместны то вероятность их суммы P(A+B)= P(A) + P(B) - P(A)*P(B)

6. Противоположные события. Вероятность появления хотя бы одного события. Примеры.

Вероятность появления хотя бы одного из событий:

7. Условная вероятность. Независимость событий. Теоремы умножения вероятностей зависимых и независимых событий.

Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной;

Если же налагаются и другие дополнительные условия, то вероятность события называют условной.

Условной вероятностью называют вероятность события , вычисленную в предположении, что событие е уже наступило.

Опр. Условная вероятность события при условии, что событие уже наступило, по определению, равна

Теорема. (Умножения двух событий). Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

(Доказательство через определение условной вероятности).

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

Пусть вероятность события В не зависит от появления события А.

Опр. Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:

Итак, если событие В не зависит от события A, то и событие А не зависит от события В; это означает, что свойство независимости событий взаимно.

Для независимых событий теорема умножения имеет вид

Опр. Несколько событий называют независимыми в совокупности (или просто независимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.

Если события независимы в совокупности, то независимы события .

8. Теорема полной вероятности. Понятие гипотезы. Формула Байеса.

Теорема. Вероятность события , которое может наступить лишь при условии появления одного из несовместных событий , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события :

Эту формулу называют «формулой полной вероятности».

Пусть событие может наступить при условии появления одного из несовместных событий , образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами.

Найдем сначала условную вероятность По теореме умножения:

.

Где имеем:

Для произвольной гипотезы

Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

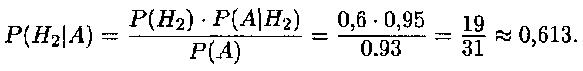
9. Схема Бернулли повторных испытаний. Наивероятнейшее число положительных исходов в схеме Бернулли.

Схема Бернулли повторных испытаний.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться или не появиться. Вероятность события А в каждом испытании одна и та же, а именно равно р. Следовательно вероятность не наступления события А равно q=1-p.

Задача: Вычислить вероятность того, что при n испытаний событие А осуществиться ровно k раз - P_n(k), причем последовательность не имеет значения.

Вывод формулы:

По теореме умножения вероятностей независимых событий, вероятность наступления события А из n испытаний k раз равна p^kq^n-k

Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k, т.е

Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность равна вероятности одного сложного события, умноженной на их число:

или

Полученную формулу называют формулой Бернулли

Наивероятнейшее число положительных исходов в схеме Бернулли.

Число k*, при котором биномиальные вероятности P_n(k*) достигают своего максимального значения (при фиксированном числе испытаний n) называют обычно наиболее вероятным наивероятнейшим числом успехов. Справедливо следующее утверждение о наивероятнейшим числе успехов:

Наивероятнейшее число успехов k* в серии из n независимых испытаний Бернулли (с вероятностью успеха р в одном испытании) определяется соотношением np-q£k*£np+p

9. Приближенные формулы вычисления вероятности в схеме Бернулли: теорема Пуассона, теоремы Муавра-Лапласа (локальная и интегральная). Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

Приближенная формула Пуассона используется в том случае, когда число испытаний Бернулли (n) – велико, а вероятность успеха в отдельном испытании мала (p<0,1). Тогда

P_n(m)»

Локальная формула Муавра-Лапласа

Если в схеме независимых испытаний Бернулли число испытаний n велико, а вероятности успеха и неудачи не малы (например, 0,1<p<0,9), то вероятность P_n(m) появления ровно m успехов в n испытаниях вычисляется по формуле:

, причем

Интегральная формула Муавра-Лапласа

Для вычисления вероятности P_n(m₁,m₂)= P(m₁£m£m₂) события, состоящего в том, что число успехов в n испытаниях Бернулли окажется заключенным в пределах от m₁ до m₂, используется следующая приближенная формула:

, причем:

• 

• - функция распределения стандартного нормального закона

• - формула Лапласа

• 

Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

Требуется найти, вероятность того, что отклонение относительной частоты m/n от постоянной вероятности р по абсолютной величине не превышает заданного числа ε>0. Другими словами, найти вероятность осуществления неравенства |m/n-p|<= ε