6. Динамика автоматизированного сцепления.

6.1. Структурная схема системы двигатель - автоматизированное сцепление и анализ ее устойчивости.

Автоматизированное сцепление - это обычное фрикционное постоянно замкнутое или разомкнутое сцепление с автоматическим приводом управления в зависимости от изменения угловой скорости вращения вала двигателя. Системы автоматического управления сцеплением могут быть: гидравлические, пневматические и вакуумные. Она представляет собой отдельный узел и может устанавливаться на автомобиль как при его сборке, так и в эксплуатации.

На рис.6.1 показана блок-схема автоматизированного сцепления.

В автоматизированных сцеплениях управление скоростью движения автомобиля осуществляется двумя педалями: топливоподачи и тормоза. Система управления сцеплением для переключения передач объединена с рычагом переключения передач в коробке передач, автоматические сцепления обуславливают конструкцию автомобиля, но полностью устраняют принудительное управление сцеплением водителем .

Автоматизированное сцепление можно представить в виде функциональной схемы [5], элементами которой являются двигатель,

регулятор, исполнительное устройство и муфта сцепления, соединенные в замкнутый контур автоматического регулирования. Задавшим сигналом является перемещение органа топливоподачи, а выходным параметром -момент трения сцепления. Перемещение органа топливоподачи приводит к появлению избыточного крутящего момента на коленчатом валу. под действием которого увеличивается угловая скорость. Регулятор преобразует изменение угловой скорости вала двигателя в сигнал, воздействующий на исполнительное устройство, которое включает сцепление, стремясь нагрузить двигатель и тем самым остановить рост угловой скорости вала. Таким образом, осуществляется отрицательная обратная связь и регулирование момента трения, но и создается опасность потери устойчивости регулирования и работоспособности

сцепления.

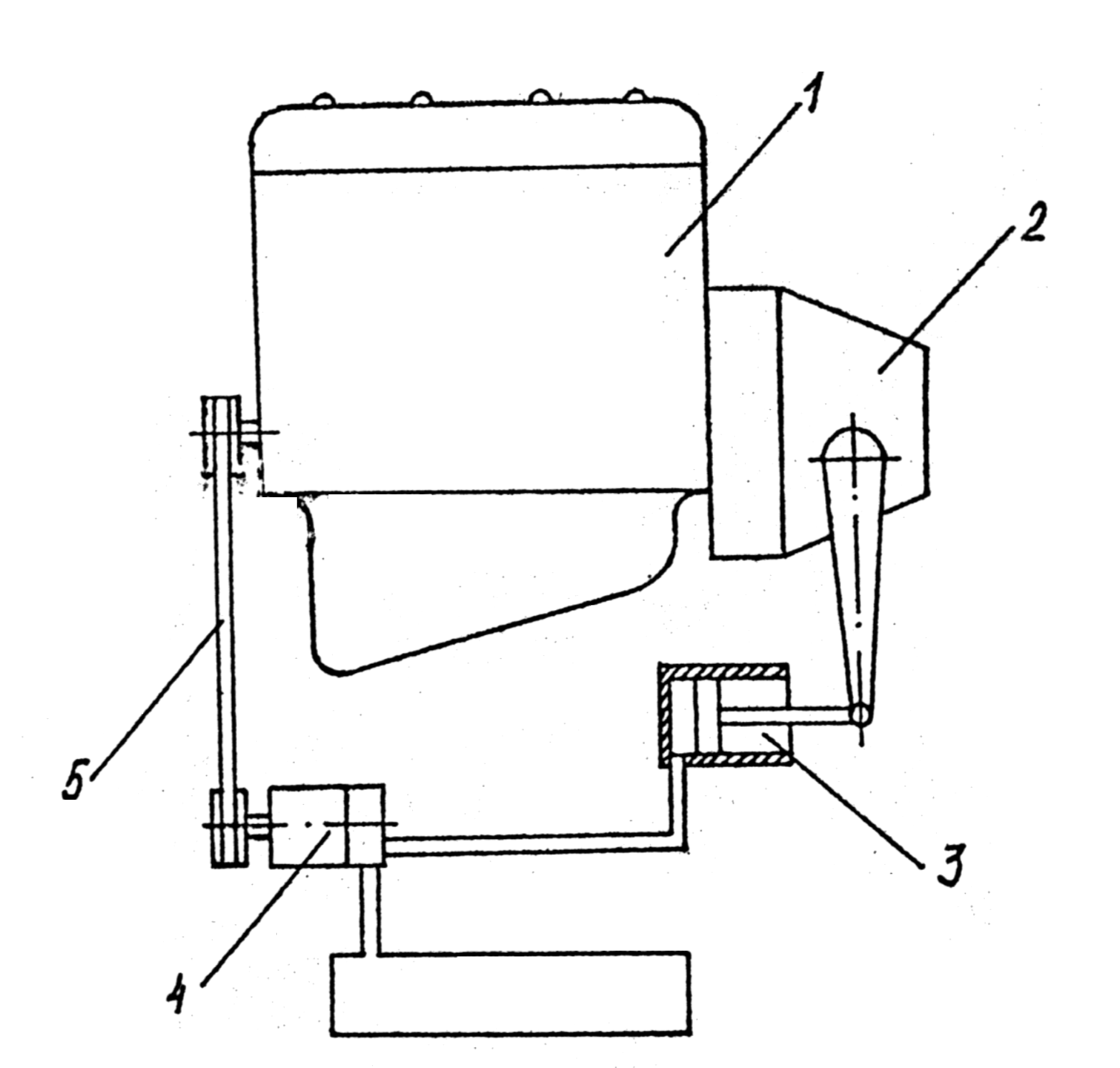
Рис.6.1. Блок-схема автоматизированного сцепления.

I – Двигатель,

2 - Сцепление,

3 - Рабочий цилиндр управления сцеплением,

4 - Регулятор давления,

5 - Привод от двигателя.

Определим условие устойчивости автоматизированного сцепления в простейшем случае моделирования его элементов:

а) передаточная функция регулятора давления

Wp = p(s)/w(s) = K_p/(T_s +1) (6.1)

б) передаточная функция исполнительного устройства

W_u = F(s) / p(s) = K_u (6.2)

в) передаточная функция муфты сцепления

W(s) = W_c (s) / F(s) = K_c (6.3)

Здесь и далее u, p, F - соответственно, угловая скорость, давление и усилие, создаваемое исполнительным устройством.

Передаточная Функция двигателя W_d может быть получена из уравнения

Jd(w)/dt + bw = W_d ,

где J - момент инерции вращающихся частей и приведенных к ним поступательно - движущихся частей двигателя; b- тангенс угла наклона статической характеристики двигателя W = f(w) к оси w. Тогда

W_d = w(s)/W_d(s) = K / T_d + 1 (6.5)

где К_d = 1/b, T_d = J/b. Эта передаточная функция соответствует двигателю, имеющему самовыравнивание, т. е. когда b > 0. При b < О двигатель лишен самовыравнивания и в этом случае

W_d = w(s)/ W_d(s) = K / T_d - 1 (6.5.1 )

Структурная схема системы "двигатель - автоматизированное сцепление" приведена на рис.6.2. Для анализа устойчивости найдем эквивалентную передаточную функцию системы и приравняем к нулю ее знаменатель, считая, что двигатель лишен самовыравнивания:

T_d T S² + (T_d + T)S + K_d K_p K_u K_c = 0

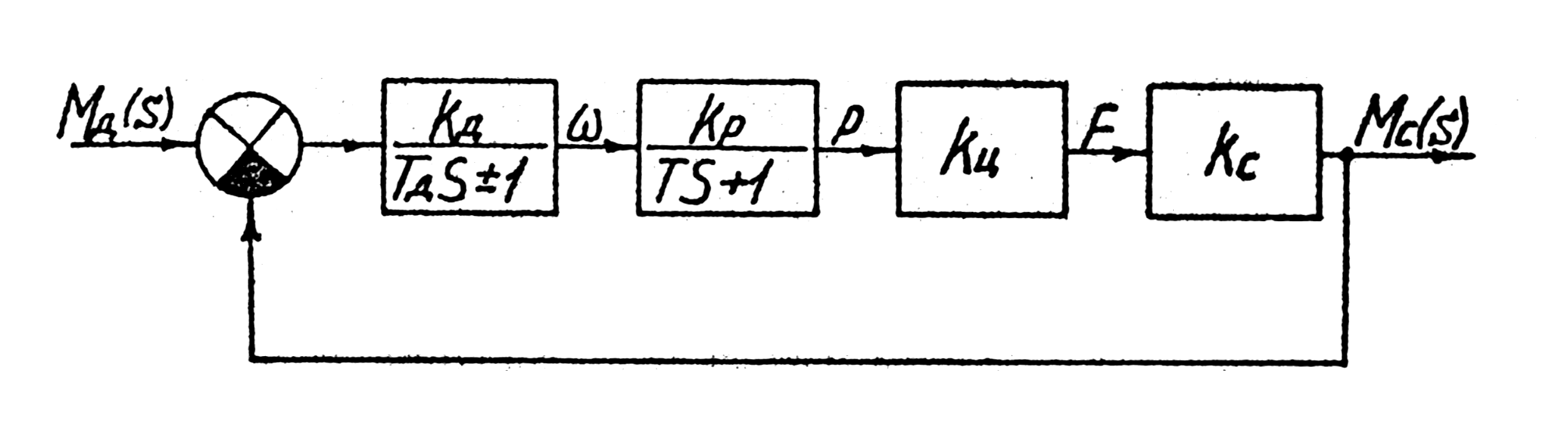
Рис. 6.2 Структурная схема системы "двигатель - автоматизированное сцепление"

В соответствии с полученным характеристическим уравнением согласно критерию Гурвица автоматизированное сцепление будет устой­чиво, если одновременно выполняются следующие условия:

T_d T > 0; T_d – T > 0; K_d K_p K_u K_c – 1 > 0

В связи с тем. что Т > 0 и Т_d > 0. условие Т Т_d > О всегда

выполняется.

Для автоматизированного сцепления условие К_d К_p К_u К_c - 1 > О такие всегда выполняется как при b < 0, так и при b > 0. Это условие статики регулирования, отражающее необходимость согласования характеристик двигателя и сцепления по моменту. Следовательно, в автоматизи­рованном сцеплении достаточно, чтобы выполнялось условие Т_d - Т > 0. Это условие динамики регулирования. Смысл его заключается в том, что регулятор автоматического сцепления должен быть менее инерционным, чем применяемый двигатель.

Обеспечение устойчивости работы автоматизированного сцепления является необходимым условием работоспособности конструкции. Однако для нормальной эксплуатации автоматизированного сцепления этого еще недостаточно. Не менее важным условием работы конструкции является получение приемлемого в эксплуатации переходного процесса включения сцепления M=f(t) при трогании автомобиля с места. Может, например, оказаться, что сцепление работает устойчиво, но переходный процесс носит колебательный характер. При этом низкочастотные колебания момента трения сцепления при трогании автомобиля с места восприни­маются пассажирами как толчки, а высокочастотные (больше 4 Гц) - как вибрации в трансмиссии автомобиля. Наиболее часто плохое качество трогания автомобиля с места объясняется малым запасом устойчивости. Характер переходного процесса зависит от корней характеристического уравнения, определяемого знаменателем передаточ­ной функции.

Если (T_d – T)² > 4T_d Т(K_d K_p K_u K_c - 1), то корни характеристичес­кого уравнения есть отрицательные действительные числа, и поэтому 'при нулевых начальных условиях переходный процесс будет аперио­дическим.

Таким образом, определены условия работоспособности и качества переходного процесса автоматизированного сцепления. Однако они получены для простой, весьма грубой модели объекта и поэтому страдают лишь общие закономерности выбора параметров. Для проектирования конкретных систем регулирования рассмотрим более строгие модели регулятора давления и исполнительного устройства с муфтой сцепления. Причем, приведенные ниже отдельные модели элементов необходимо рассматривать в составе структурной схемы "двигатель - автоматизированное сцепление".