5.3. Исполнительный элемент

В качестве исполнительных элементов чаде всего используют гидравлические и пневматические поршневые цилиндры и мембранные камеры. Здесь выходной параметр - перемещение штока, а входная величина – давление, подаваемое в рабочую полость.

Тогда передаточная функция элемента будет иметь вид

W(s) = X(s)/p(s) = f/(m s² + v s + с). (5.6)

где m - масса подвижных частей исполнительного механизма.

f - эффективная площадь поршня.

u - коэффициент вязкого трения

с - жесткость возвратной пружины.

5.4. Центробежный механизм

На автомобилях и тракторах центробежные механизмы используются весьма широко: в автоматизированных приводах сцеплений, центробежных сцеплениях, системе зажигания карбюраторных двигателей, регуляторах частот вращения двигателей, автоматических гидропередачах.

Центробежные механизмы имеют такие положительные свойства, как получение больших усилий на управляющем органе, простота конструкции, надежность, стабильность в работе (на работу не влияют окружающая температура, давление воздуха, вибрации), большое быстродействие, малая приводная мощность. Они широко применятся в регуляторах давления и других следящих устройствах. Бывают двух типов: рычажный и безрычажный.

На рис.5.2 показан рычажный центробежный механизм. Из условия равновесия грузов сила. приложенная к штоку механизма в результате действия центробежной силы грузов будет иметь вид

F = Fu w R i

где i - передаточное число рычагов.

Центробежные механизмы могут проектироваться так, что

а) R i = const.

б) R i  const.

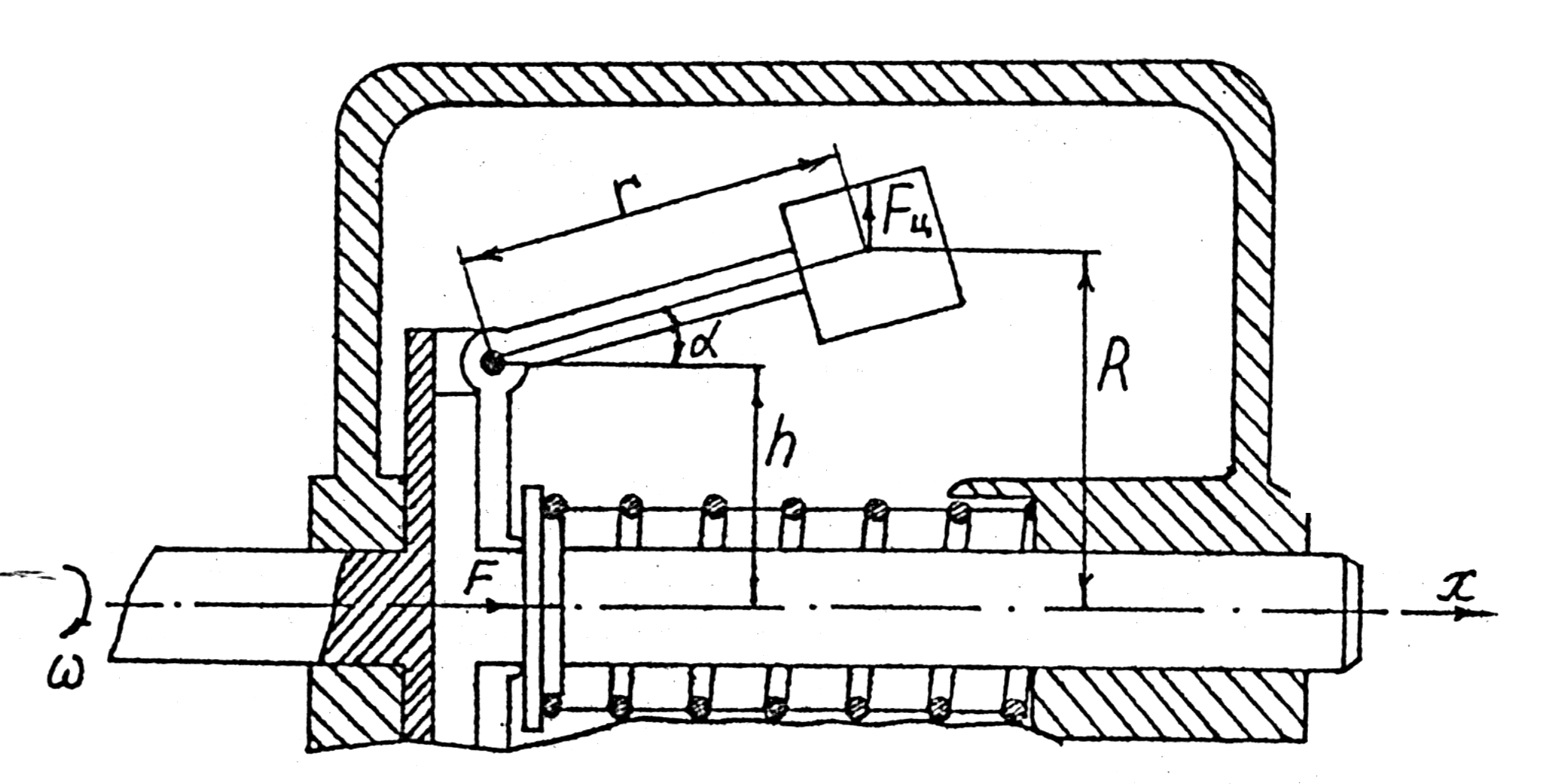
Рис.5.2. Схема рычажного центробежного механизма.

Рассмотрим оба случая.

1 случай: Ri = const. Тогда при изменении частоты вращения на

dw (w = w₀ + dw) можно написать дифференциальное уравнение в приращениях следующим образом:

m(dX)ⁿ + v dX)¹ + c(dX) = dF (5.7)

где m - приведенная масса поступательно - движущихся частей: v - коэф­фициент вязкого трения; с - жесткость возвратной пружины. С учетом того, что dF = m Ri (dw)² = m Ri 2 w₀ dw, преобразуем дифференциальное уравнение по переменной время t и, преобразовав последнее уравнение в уравнение в операторной форме по переменной s:

(mS² + vS + c) X (s) = 2m Ri w₀ w(s) = K w(s)

где К = 2m, Ri w₀ - коэффициент усиления центробежного меха­низма. Тогда передаточная функция центробежного механизма будет иметь вид -

W(s) = X(s)/w(s) = K/(ms² + vs + c) (5.8)

из чего следует, что центробежный механизм является колебательным звеном.

Полученную передаточную функцию можно представить в виде двух последовательно соединенных типовых динамических звеньев:

- усилительного с передаточной функцией W (s) = F (s)/W(s) = К,

- колебательного W (s) = X(s)/F (s) = 1/(ms² + vs + с).

Условие устойчивости центробежного механизма можно определить по критерию Гурвица как для уравнения третьего порядка

m > 0, v > О, с > 0.

Отсюда видно, что такой центробежный механизм всегда устойчив.

Условия, при которых Ri = const. Из схемы для рычажного центробежного механизма имеем:

R = h + r Sin(a); а = r Cos(a); и i = r Cos(a)/b; i = а/b.

Тогда Ri = {[h + г Sin(a)] r Cos(a)}/b,

откуда Ri b/r = (h/r) Cos(a) + Sin(a) Cos(a).

Для получения условий, при которых Ri = const. найдем производную полученного выражения по углу (a) и приравниваем ее к нулю:

(h/r)(-Sin(a)) + Cos(a) Cos(a) - Sin(a) Sin(a) =

= - (h/r) Sin(a) + Cos2(a) =0

Так как отношение h/r > 0, то всегда угол (a) < 45 . После расчета, получим следующую таблицу:

отношение h/r 0.5 1.0 2.0 3,0 4.0 

угол (a) 37 30 26 22 17 0

2 случай: Ri  const. но i = const. Тогда можно записать

dF = d(m Ri w) = m i R d(w) + m i w₀ d( R)

Далее полагая, что при малых перемещениях штока

R = Xi

и подставляя все в дифференциальное уравнение получим

m(dX)ⁿ + v (dX) + (c – m iw₀) (dX) = 2mRi w₀d(w)

Здесь 2mRiw₀ = Km- .коэффициент усиления центробежного механизма, а (с – m i w₀) = C₃ - эквивалентная жесткость пружины на штоке центробежного механизма.

Тогда передаточная функция такого центробежного механизма будет иметь вид

W( ) = X(s)/w(s) = K_m /(ms + vs + с₃) (5.9)

Таким образом, для центробежного механизма с Ri  const вместо С следует рассматривать С₃- эквивалентную жесткость пружины, которая называется коэффициентом самовыравнивания или фактором устойчивости, так как для устойчивости необходимо, чтобы:

(c – m i w₀) > 0, то есть с > m i w₀ .

Следовательно только при определенных значениях параметров с, m , i и w₀ центробежный меха­низм будет устойчив.