4. Устойчивость автоматических систем

4.1. Понятие устойчивости линейных систем

Различные возмущающие силы вызывают отклонение выходной величины, нарушая устойчивое состояние системы. Для того, чтобы автоматическая система могла выполнять предписанные ей функции, то есть иметь требуемый переходный процесс, необходимо обеспечить устойчивое его протекание.

Под устойчивой системой понимают такую, которая при отклонении от состояния равновесия под действием возникающих в ней внутренних воздействий стремится вернуться в состояние равновесия.

Соответственно, неустойчивой является система, которая под

влиянием возмущения отклоняется от состояния равновесия, а после прекращения действия возмущения не возвращается к исходному равновесному состоянию. При этом удаление системы от первоначального состояния с течением времени возрастает настолько, что отклонение выходит за пределы допустимой величины. Неустойчивый объект регулирования - такой объект, который регулирования не может самостоя­тельно вернуться к равновесному состоянию.

Понятие устойчивости наглядно иллюстрируется схемами на рис.4.1.

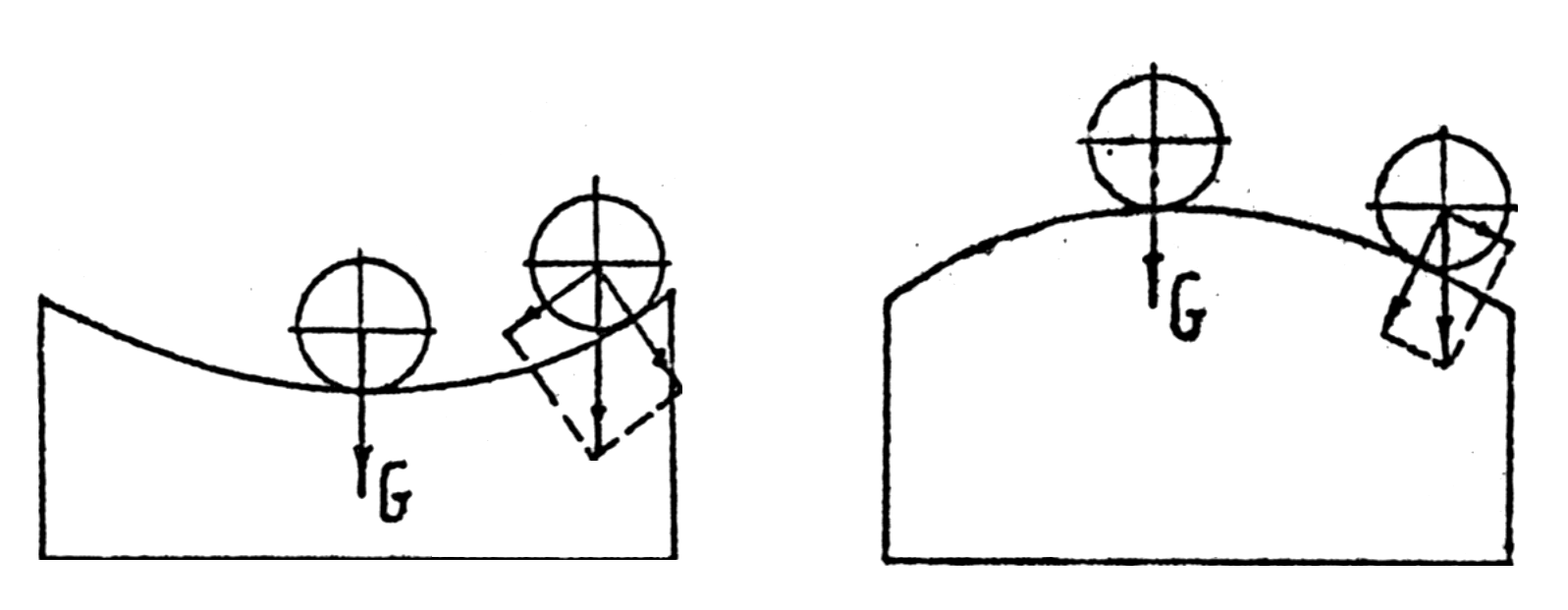
а б

Рис.4.1. Схемы, иллюстрирующие устойчивость объекта.

а – устойчивая система,

б – неустойчивая система.

Первое математически строгое понятие устойчивости движения сформулировал А.М.Ляпунов в 1892 г. Для этого он представил закон изменения во времени выходной величины Y(t) в виде

Y(t) = Yc(t) + Yb(t). (4.1)

где Y(t) и Yс(t) - составляющие, соответственно, свободного и вынужденного движения, определяемые возмущающими воздействиями, начальными условиями, свойствами самой системы.

Для устойчивости необходимо, чтобы с течением времени предел limYc(t) —> 0, то есть при Yb(t) = 0 стремилась к нулю свободная составляющая переходного процесса Yс(t).

Уравнение свободного движения линейной автоматической ситемы, когда внешние воздействия отсутствуют, является линейным однородным и в операторной форме имеет вид [2]:

(A₀Sⁿ + A₁ S^n-1 … A_n-1S + A_n)Y₀(s) = 0 (4.2)

где Yc(t) и Yb(t) - постоянные коэффициенты уравнения.

Ус ts) - операторное изображение выходной величины для составляющей свободного движения системы.

Решение однородного дифференциального уравнения имеет вид [2], где

Yc(t) = ⁿ Aj * e ^s_j^t; (4.3)

^{i =1}

где A - постоянные интегрирования, определяемые параметрами системы и начальными условиями,

t - текущая координата времени,

s - корни характеристического уравнения, которые могут быть действительными или комплексными,

J - номер корня s и постоянной А,

n - степень уравнения, численно равная порядку дифференциаль­ного уравнения.

Если все корни характеристического уравнения вещественные, то составляющая уравнения (4.3) представляет собой экспоненту, вид которой зависит от знака показателя степени, то есть знака корня s:

а) если корень s отрицателен, то экспонента стремится к нулю,

б) если корень s положителен, то экспонента стремится к бесконечности,

в) если корень s = 0. то экспонента изображается прямой линией, параллельной оси абсцисс.

Если все корни уравнения комплексные, то переходный процесс будет колебательным и на основании преобразования Эйлера уравнение (4.3) можем записать следующим образом:

A_je^s_j^t = A_je^(a_j^{i b}_j^)t = e^a_j [cos(b_jt) + i sin(b_jt)] (4.4)

Наличие периодических функций говорит о колебательном характере переходного процесса, а вид колебаний определяется знаком показателя степени числа е, то есть знаком вещественной части a_j корня характеристического уравнения системы ;

а) если а отрицательна, то колебания затухают, стремясь с течением времени к нулю,

б) если а положительна, то колебания нарастают, стремясь к бесконечности.

в) если a_j = 0, то е колебания постоянны и не затухают.

Отсюда условие устойчивости по Ляпунову:

1) Если все корни характеристического уравнения имеют отрицатель­ные вещественные части (корни характеристического уравнения располагаются слева от мнимой оси на комплексной плоскости), то система устойчива.

2) Если среди корней характеристического уравнения есть хотя бы один корень с положительной вещественной частью, то система не устойчива.

Из этого следует, что на комплексной плоскости корни расположенные в левой полуплоскости комплексной плоскости, то есть слева от мнимой оси, соответствуют устойчивому состоянию, а справа от мнимой оси соответствуют неустойчивому состоянию.

Таким образом, для определения устойчивости системы нужно уметь находить корни характеристического уравнения. Это делается просто для уравнений первого и второго порядка, сложней для уравнений третьего порядка, а уравнения высоких порядков не имеет решения в общем виде. Поэтому разработаны косвенные критерии устойчивости системы. Они называются алгебраическими критериями устойчивости.