3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ АВТОМАТИЧЕСКОЙ СИСТЕМЫ
3.1. Структурная схема системы
Для анализа динамических характеристик в большинстве случаев значительно быстрее, проще и полезнее математическое описание автоматической системы формировать не на основе системы уравнений элементов, а путем построения так называемой структурной схемы при помощи аппарата передаточных функций типовых звеньев. Структурная (алгоритмическая) - схема - это условное графическое изображение автоматической системы. Она характеризует геометрию системы, пути распространения сигналов, определяет из каких динамических звеньев состоит автоматическая система и как они связаны между собой. На структурную схему наносятся условными знаками все динамические звенья в виде прямоугольника с обозначением их передаточных функций, связей и направлений распространения сигналов в виде стрелок, точек разветвления и сумматоров сигналов, изображения входной и выходной величин, изображения внешних воздействий.
Таким образом, структурная схема показывает строение автоматической системы, наличие внешних воздействий и точки их приложения, пути распространения воздействий, входную и выходную величины. По структурной схеме можно составить математическое описание автоматической системы, составить передаточную функцию всей системы и построить график переходного процесса. При таком начертании структурная схема автоматической системы представляет собой графическое изображение системы дифференциальных уравнений, описывающих работу автоматической системы. Графическое изображение предпочтительнее обычной математической записи уравнений, так как позволяет весьма просто и, пользуясь формальными единообразными правилами, производить "свертывание" этих уравнений для получения математической модели системы (передаточной функции всей системы) в удобной для анализа форме.
На рис. 3.1 и 3.2 показан пример структурной схемы автоматической системы регулирования скорости вращения электрического двигателя.
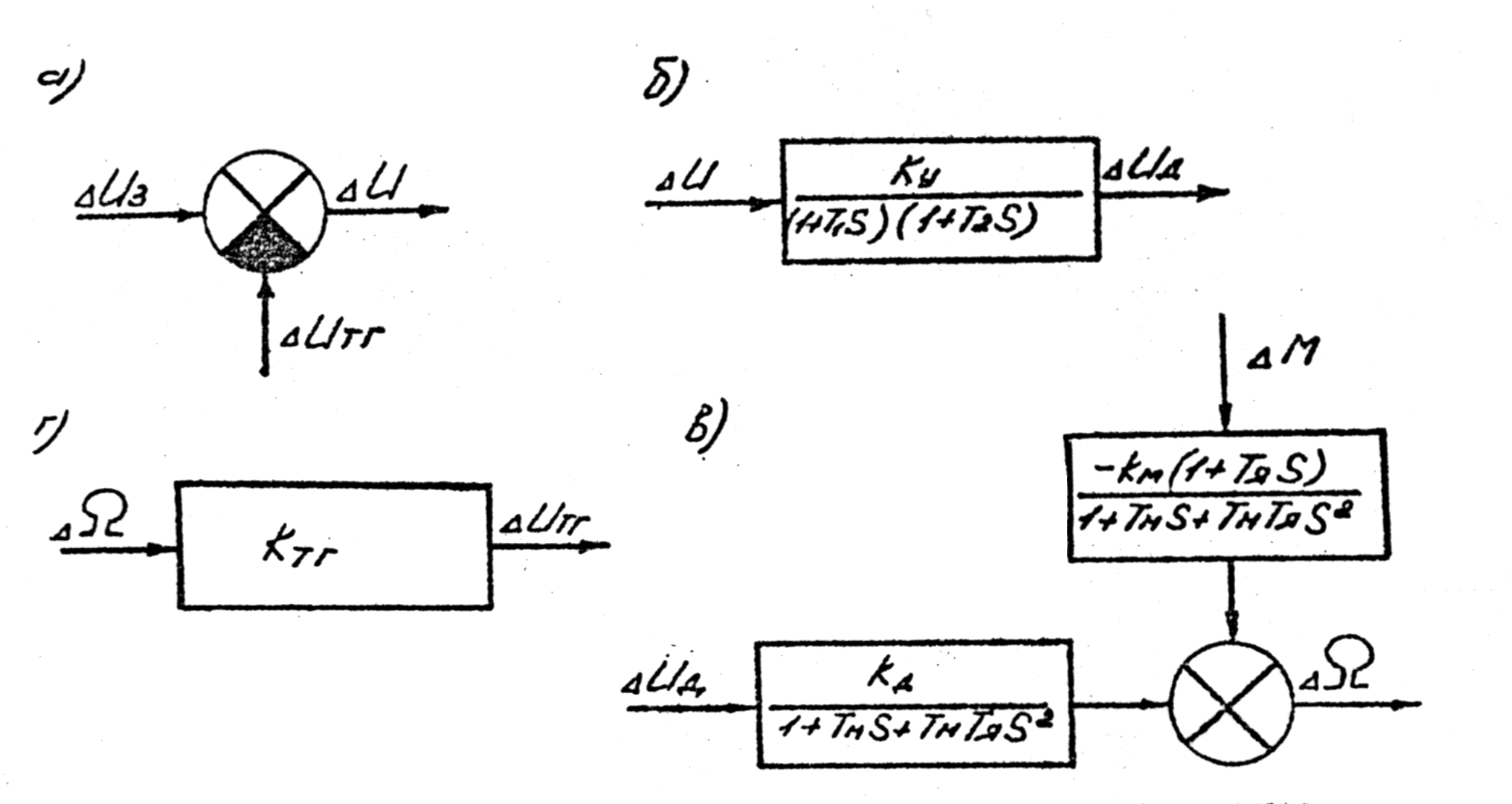
Рис. 3.1. Передаточные функции звеньев системы регулирования скорости вращения электрического двигателя.
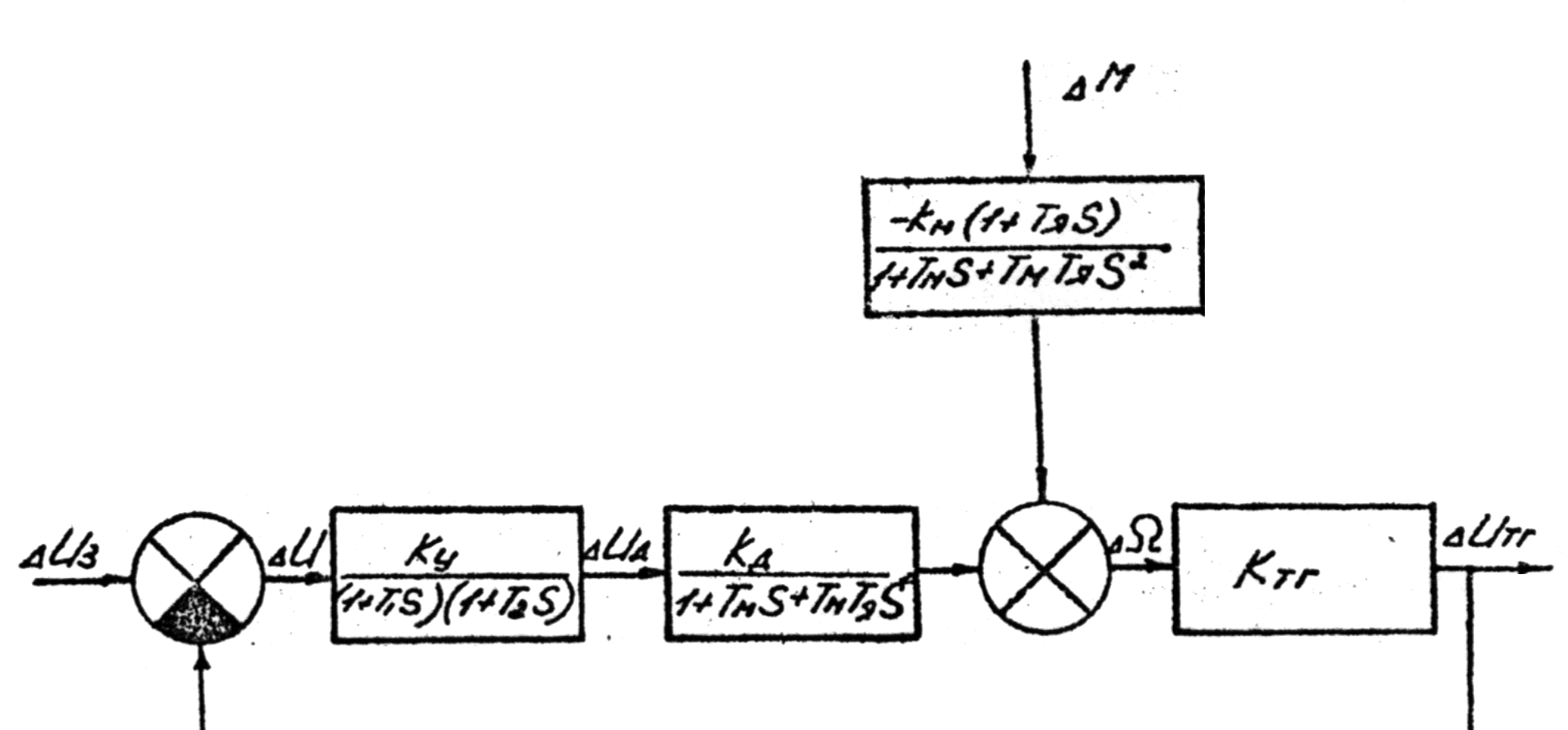
Рис.3.2. Структурная схема автоматической системы регулирования скорости вращения электрического двигателя.
Составление схемы удобно начинать с изображения задающего воздействия и располагать динамические звенья в прямой связи слева направо до регулируемой величины, а затем (или одновременно) показывать местные и главную обратные связи.
Существует три основных типа соединений динамических звеньев:
- последовательное соединение двух и более звеньев,
- параллельное соединение двух звеньев с общим входом.
- встречно-параллельное соединение звеньев или соединение звеньев с обратной связью.
Каждое типовое соединение звеньев можно заменить одним эквивалентным звеном с соответствующей эквивалентной передаточной функцией по установленным правилам. Для типовых соединений такая передаточная функция равна;
а) при последовательном соединении - произведению передаточных функций звеньев
W(S) = Пn Wi,(S); (3.1)
i=1
б) при параллельном соединении (входная величина одна и та же для всех элементов данного соединения, а выходные величины разные и суммируется) : - сумме передаточных функций звеньев.
W(S) = n Wi(S); (3.2)
i =1
в) при встречно - параллельном соединении (с отрицательной обратной связью) сигнал Y(s) с выхода звена с передаточной функцией W(S) подается обратно на его вход через другое звено с передаточной функцией W2(S) как показано на рис.3.3. Здесь на входе мы имеем сумму сигналов X(s) – W2(S) Y(S). По определению передаточной функции для элемента в прямой связи
W(S) = Y(S)/[Х(S) - W2(s)*Y(S)]
Отсюда передаточная функция такого соединения равна:
W(S) = W2(S)/[l – W1(S)W2(S)] (3.3)
Таким образом, эквивалентная передаточная функция встречно-параллельного соединения равна дроби, числитель которой -произведение передаточных функций прямой связи, а знаменатель -произведение передаточных функций пряхой и обратной связей, взятое с противоположным знаком сумматору в обратной связи, плюс единица.
В структурных схемах могут быть и другие соединения звеньев, которые отличаются от типовых соединений и по ним нельзя составить эквивалентную передаточную функцию. В этом случае производят преобразования отдельных частей структурной схемы для получения типовых соединений звеньев. Имеется много правил преобразования не типовых соединений звеньев. Рассмотрим некоторые из них. На рис.3.4 показаны схемы следующих преобразований:
а) Перенос точки разветвления через звено с добавление в ответвляющуюся связь звена, через которое переносили эту точку разветвления (Рис.3.4а и 3.4б): звено с передаточной функцией 1/W(S) при переносе по направлению распространения сигнала и звено с передаточной функцией W(S) при переносе против направления распространения сигнала.
б) Перенос сумматора через звено с добавлением в ответвляющуюся связь звена, через которое переносили сумматор (Рис.3.4в и 3.4г):
звено с передаточной функцией W(S) при переносе по направлению распространения сигнала и
звено с передаточной функцией l/W(S) при переносе против направления распространения сигнала.
Перестановка между собой соседних точек разветвления, находящихся между звеньями не приводит к изменению схемы. При перестановке между собой соседних сумматоров схема также не изменяется.
Преобразование структурных схем должно осуществляться в следующей последовательности:
1) Замена каждого типового соединения звеньев в схеме эквивалёнтным звеном, выражая его эквивалентной передаточной функцией через передаточные функции типовых звеньев.
2) Последовательное преобразование не типовых соединений звеньев в типовые соединения звеньев с последующим их преобразованием.
Каждая операция выполняется последовательно одна за другой до получения эквивалентной одноконтурной схемы, по которой составляется передаточная функция всей системы.
Здесь рассмотрены простейшие структурные преобразования. Обычно с их помощью удается многоконтурную структурную схему привести к одноконтурной.
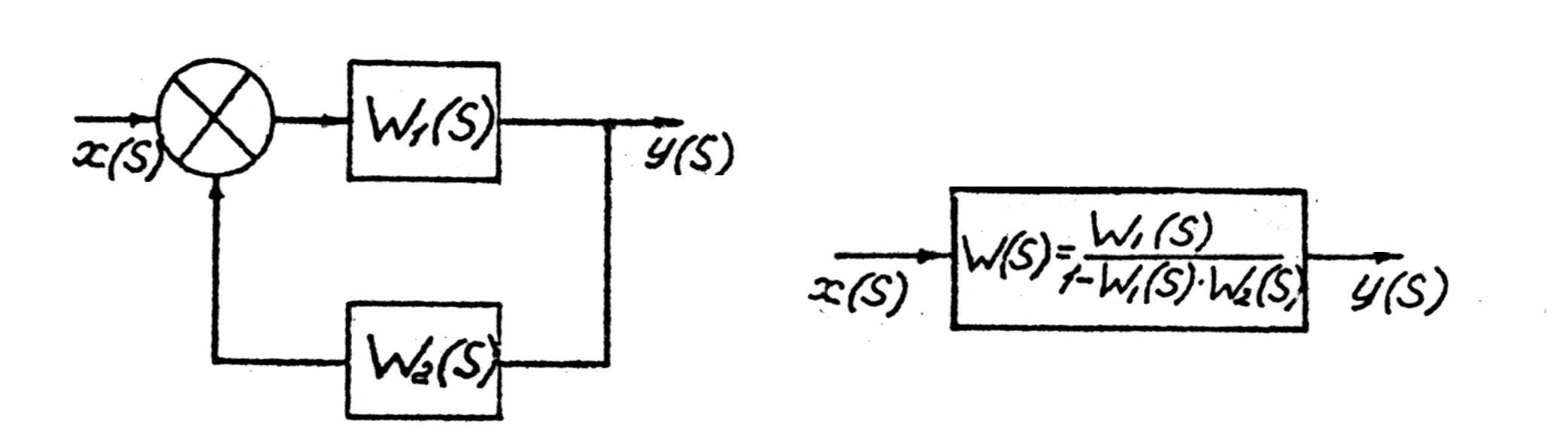
Рис.3.3. Встречно – параллельное соединение звеньев.
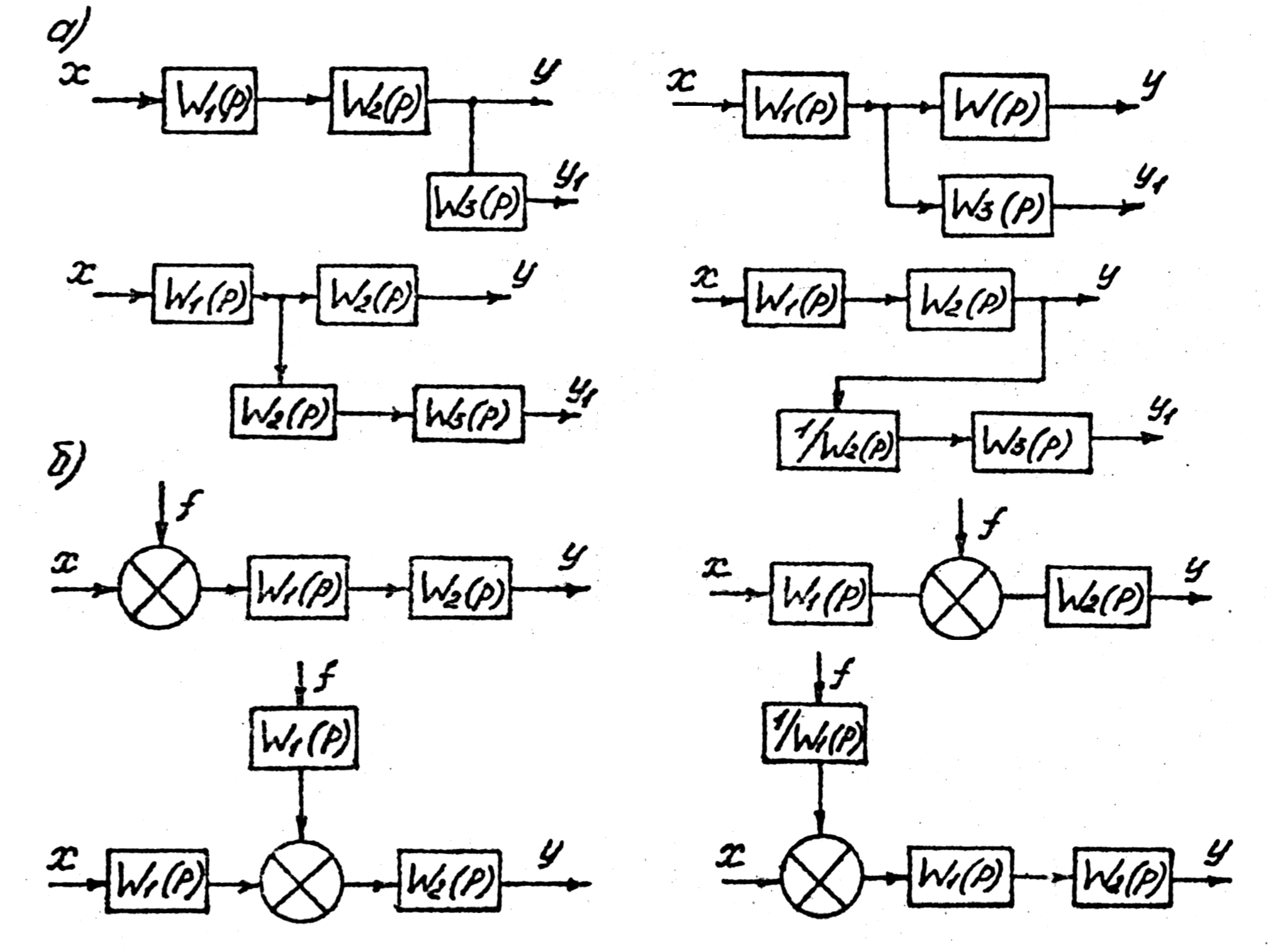
Рис.3.4. перенос точек разветвления и сумматоров.
3.2. Некоторые передаточные функции линейных систем.
При расчете и анализе автоматических систем составляют передаточные функции относительно различных выходных величин:
выходной величины всей системы, задавшего воздействия, каждого из возмущений, для ошибки слежения. Найдем значения этих передаточных функций для структурной схемы, показанной на рис.3.5.
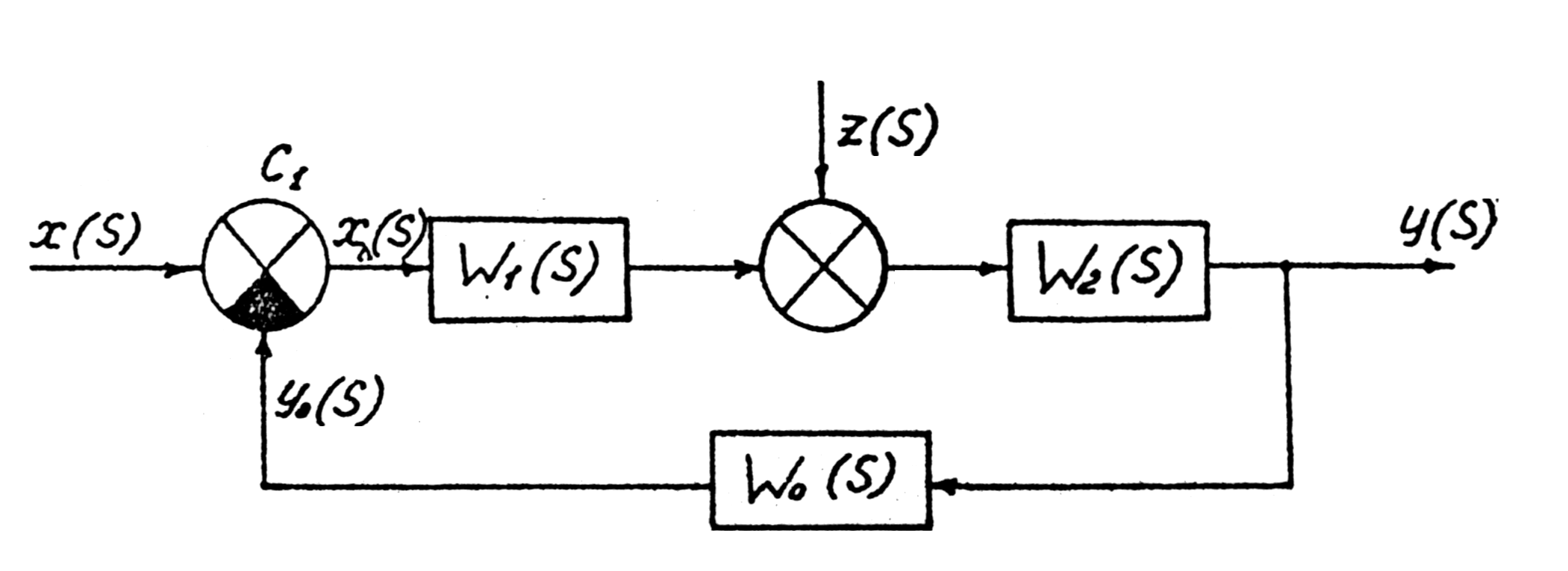
Рис.3.5. Структурная схема.
Для разомкнутой системы, которая разомкнута около элемента сравнения (сумматора С1):
W(s) = Yo(s)/X(s) = W1(s) W2(s) Wo(S). (3.4)
Где Y0(s) - изображение сигнала обратной связи, X(s) - изображение задавшего воздействия. Эта передаточная функция характеризует собственные динамические свойства системы и по ней определяет ее устойчивость.
2) Для замкнутой системы относительно входного воздействия Х(s) предполагая, что других внешних воздействий нет:
W(s) = Y(s)/X(s) = W1(s)W2(s)/[1+W1(s)W2(s)W0(s) (3.5)
где Y(s) - изображение регулируемой величины. X(s) - изображение задавшего воздействия.
Эта передаточная функция характеризует передачу системой задавшего воздействия, его воспроизведение регулируемой величиной.
3) Для замкнутой системы по ошибке сложения, предполагая, что других внешних воздействий нет:
W(S) = ХD(S)/Х(S) = 1/[1 + W1(S) W2(S) W0(S)]. (3.6)
где ХD(S) - изображение рассогласования ХD(S) = X(s) - Yo(S).
Здесь в прямой связи нет звеньев. Формула характеризует воспроизведение регулируемой величиной заданного воздействия. Воспроизведение тем лучше, чем ближе значение W(s) к идеальному, то есть нулю.
4) Для замкнутой системы относительно возмущения Z(s) при отсутствии других внешних воздействий:
W(s) = Y(s)/Z(s) = W(s)/[l + W1(s) W2(s) W0(s)] (3.7)
где Z(s) - изображение возмущения.
Формула показывает влияние возмущения на регулируемую величину. Возмущение отклоняет ее от заданного значения и уменьшает точность воспроизведения задающего воздействия. Если на систему воздействует несколько возмущений, то передаточная функция определяется относительно каждого из них.
5) Для системы относительно задающего воздействия X(s) и возмущения Z(s):
Y(s) = Wx(s)X(s) + W2(s) Z(s). (3.8)