69 Зведення матричної гри до задачі лінійного програмування

Якщо матрична гра не має сідлової точки, то знаходження її розв’язку, особливо за великої кількості стратегій, – доволі складна задача, яку можна ефективно розв’язати методами лінійного програмування.

Задача розглядається в такому формулюванні: знайти вектори ймовірностей з метою визначення оптимального значення ціни гри та оптимальних стратегій.

Зауважимо, що доведено основну теорему теорії ігор: кожна скінчена гра має принаймні один розв’язок, який можливий в області змішаних стратегій.

Отже, нехай маємо скінченну матричну гру з платіжною матрицею

.

Оскільки оптимальні стратегії гравців А і В дозволяють отримати виграш

,

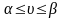то використання оптимальної змішаної стратегії гравцем А має забезпечувати виграш не менший за ціну гри в разі вибору гравцем В будь-яких стратегій. Математично ця умова записується так: 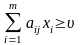. (10.1)

Відповідно використання оптимальної змішаної стратегії гравцем В має за будь-яких стратегій гравця А забезпечувати програш В, що не перевищує ціни гри 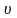: 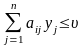. (10.2)

Ці два співвідношення застосовують для знаходження розв’язку гри.

Отже, потрібно знайти 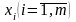, щоб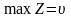

за умов , , .

Зауважимо, що ціна гри невідома і має бути визначена під час розв’язування задачі.

Модель ігрової задачі може бути спрощена.

З (10.1) маємо:

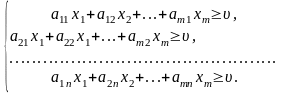
Поділивши всі обмеження на , дістанемо:

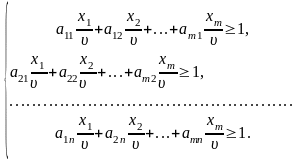
Нехай 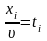, тоді

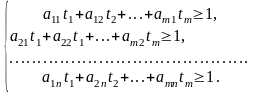
Згідно з умовою 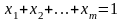, звідки .

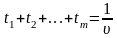Отже, цільова функція початкової задачі набирає такого вигляду:

.

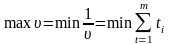У результаті задача лінійного програмування: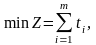 (10.3)за умов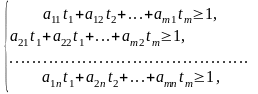 (10.4) 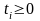. (10.5)

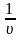Розв’язавши цю задачу симплексним методом, знайдемо значення , а також і 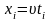, тобто визначимо змішану оптимальну стратегію для гравця А.

За аналогією запишемо задачу лінійного програмування для визначення оптимальної стратегії гравця В. Нехай

.

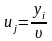Тоді маємо таку лінійну модель:

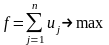
за умов

.

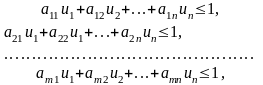
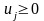Очевидно, що задача лінійного програмування для гравця В є двоїстою до задачі гравця А, а тому оптимальний розв’язок однієї з них визначає оптимальний розв’язок спряженої.

Задачі теорії ігор належать до задач прийняття рішень за умов невизначеності та ризику.

Невизначеність результатів гри зумовлена кількома чинниками. По-перше, як правило, кількість можливих варіантів розвитку подій дуже велика, тому передбачити результат гри неможливо. Простою ілюстрацією такого твердження є гра в шахи. Із-за безлічі можливих комбінацій знайти оптимальний розв’язок такої гри неможливо. По-друге, значний вплив на хід та результати гри мають випадкові чинники, дію яких передбачити неможливо, наприклад, у рулетці. По-третє, джерелом невизначеності є брак інформації щодо дій противника. Крім того, невизначеність певною мірою може стосуватися також і мети, якої прагне досягти суб’єкт. Не завжди таку мету можна виразити однозначно, а тим більше одним показником.

Зрозуміло, що коли початкові умови задачі містять значну кількість невизначених параметрів, то математичне досліджен ня не може дати чіткого обґрунтування раціонального роз в’язку, однак і за відсутності повної визначеності кількісний аналіз дає наукову основу для прийняття рішень. Т. Сааті – засновник науки «Дослідження операцій» (інструментарієм якої є «Математичне програмування») писав, що «Дослідження операцій» – це таке мистецтво, яке дає погані відповіді на такі практичні запитання, на які інші методи дають ще гірші відповіді.

Отже, уможливлюючи розв’язування задач за умов невизначеності, навіть якщо неможливо знайти точний оптимальний розв’язок, математичні методи, в тому числі і методи теорії ігор, являють собою допоміжний матеріал, який дає змогу в складній ситуації оцінити кожен з можливих варіантів розвитку

70. Теоретичні основи геометричної інтерпретації ігрової ситуації.

Решение игр размера 2xn или nx2 допускает наглядную геометрическую интерпретацию. Такие игры можно решать графически.

Дадим геометрическую интерпретацию игры, рассмотренной выше в рамках примера 5.3.

На плоскости XY по оси абсцисс отложим единичный отрезок A₁A₂ (рисунок 5.1). Каждой точке отрезка поставим в соответствие некоторую смешанную стратегию U = (u₁, u₂). Причем расстояние от некоторой промежуточной точки U до правого конца этого отрезка – это вероятность u₁ выбора стратегии A₁, расстояние до левого конца - вероятность u₂ выбора стратегии A₂. Точка А₁ соответствует чистой стратегии А₁, точка А₂ – чистой стратегии А₂.

В точках А₁ и А₂ восстановим перпендикуляры и будем откладывать на них выигрыши игроков. На первом перпендикуляре (совпадающем с осью OY) покажем выигрыш игрока А при использовании стратегии А₁, на втором – при использовании стратегии A₂. Если игрок А применяет стратегию A₁, то его выигрыш при стратегии B₁ игрока B равен 2, а при стратегии B₂ он равен 5. Числам 2 и 5 на оси OY соответствуют точки B₁ и B₂. Аналогично на втором перпендикуляре найдем точки B^'₁ и B^'₂ (выигрыши 6 и 4).

Соединяя между собой точки B₁ и B^'₁, B₂ и B^'₂, получим две прямые, расстояние от которых до оси OX определяет средний выигрыш при любом сочетании соответствующих стратегий.

Например, расстояние от любой точки отрезка B₁B^'₁ до оси OX определяет средний выигрыш игрока A при любом сочетании стратегий A₁ и A₂ (с вероятностями u₁ и u₂) и стратегии B₁ игрока B.

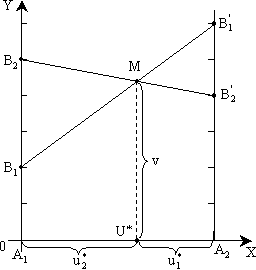
Рисунок 5.1 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока А)

Ординаты точек, принадлежащих ломаной B₁MB^'₂ определяют минимальный выигрыш игрока A при использовании им любых смешанных стратегий. Эта минимальная величина является наибольшей в точке М, следовательно, этой точке соответствует оптимальная стратегия U^* = ( ,  ), а ее ордината равна цене игры v.

Координаты точки M найдем, как координаты точки пересечения прямых B₁B^'₁ и B₂B^'₂.

Для этого необходимо знать уравнения прямых. Составить такие уравнения можно, используя формулу для уравнения прямой, проходящей через две точки:

Составим уравнения прямых для нашей задачи.

Прямая B₁B^'₁:

=     или   y = 4x + 2.

Прямая B₂B^'₂:

=     или   y = -x + 5.

Получим систему:

y = 4x + 2, y = -x + 5.

Решим ее:

4x + 2 = -x + 5, 5x = 3, x = 3/5, y = -3/5 + 5 = 22/5.

Таким образом, U^* = (2/5, 3/5), v = 22/5.

Аналогично решается задача по нахождению оптимальной стратегии игрока B. Разница состоит в том, что находится точка, сводящая к минимуму средний проигрыш, поэтому на рисунке 5.2 рассматривается ломаная A₂MA^'₁.

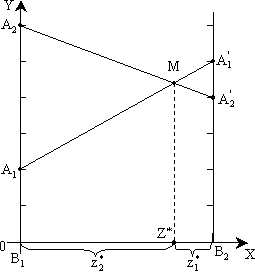
Рисунок 5.2 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока B)

Найдем координаты точки М.

Прямая A₁A^'₁:

=   ,  откуда  y = 3x + 2.

Прямая A₂A^'₂:

=   ,  откуда  y = -2x + 6,

3x + 2 = -2x + 6, 5x = 4, x = 4/5.

Таким образом,   = 1/5,   = 4/5.

В общем случае схема решения игры 2xn или nx2 графическим методом состоит в следующем.

1. Строят прямые, соответствующие стратегиям второго (первого) игрока.

2. Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой. Эти стратегии являются активными в оптимальной смешанной стратегии второго (первого) игрока.

3. Находят координаты точки пересечения, тем самым определяя оптимальную стратегию первого (второго) игрока и цену игры.

4. Оптимальную стратегию другого игрока находят, решая систему уравнений, включающую его активные стратегии.

Пример 5.4. Найдите решение игры, заданной матрицей:

A =

7    9   8 10   6   9

.

Решение.

Сначала проверим наличие седловой точки:   = 7,   = 9. Поскольку нижняя и верхняя цены игры не совпадают, седловая точка отсутствует, и решение следует искать в смешанных стратегиях.

Выполним построения на плоскости XY в соответствии с методикой, приведенной выше. Результат представлен на рисунке 5.3.

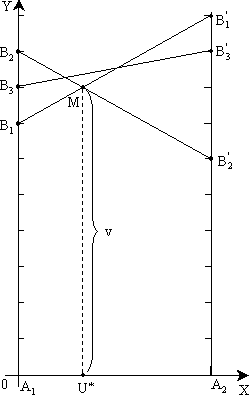
Рисунок 5.3 – Геометрическая интерпретация игры примера 5.4

Точка М находится на пересечении отрезков, соответствующих стратегиям B₁ и B₂ второго игрока.

Найдем ее координаты:

B₁B^'₁:

=   ,  откуда  y = 3x + 7,

B₂B^'₂:

=   ,  откуда  y = -3x + 9,

3x + 7 = -3x + 9, 6x = 2, x = 1/3, т.е.   = 2/3,   = 1/3, цена игры v = 8.

Активными стратегиями игрока B являются стратегии B₁ и B₂, следовательно,   = 0.

Используя выражение (5.2), вытекающее из теоремы об активных стратегиях, составим систему из двух уравнений с двумя неизвестными:

7  + 9  = 8,  +   = 1.

Второе уравнение умножим на семь и вычтем из первого:

2  = 1,  = 1/2,     = 1/2.

Ответ: U^* = (2/3, 1/3); Z^* = (1/2, 1/2, 0); v = 8.