- •Сутність поняття “модель”. Особливості математичної моделі
- •Сутність методології математичного моделювання. Узагальнена схема математичного моделювання
- •Особливості і принципи математичного моделювання
- •Поняття економіко-математичної моделі. Узагальнена схема процесу математичного моделювання економічних процесів.
- •Особливості процесу математичного моделювання економічних систем. Особливості економічних спостережень і вимірів.
- •Практичні завдання економіко-математичного моделювання. Роль математичних методів в економіці.
- •Охарактеризуйте основні етапи економіко-математичного моделювання. Етапи економіко-математичного моделювання
- •8 Основні засади щодо класифікації економіко-математичних моделей. Наведіть приклади та дайте відповідні пояснення.
- •9. Сутність аналітичного та комп’ютерного моделювання.
- •10. Роль прикладних економіко-математичних досліджень.
- •11. Взаємозв’язкок валідації, верифікації та забезпечення довіри до моделі.
- •12. Постановка задачі економіко-математичного моделювання. Сутність понять: «параметри», «змінні», «цільова функція», «система обмежень».
- •14. Предмет математичного програмування. Приклади економічних задач математичного програмування.
- •15. Багатокритеріальна оптимізація економічних систем. Навести відповідні формули.
- •16. Класифікація задач математичного програмування
- •17. Постановка транспортної задачі та методи її розвязання
- •18. Алгоритм розв’язання транспортної задачі методом потенціалів
- •20. Методи побудови першого опорного плану транспортної задачі: мінімальної вартості; апроксимації Фогеля
- •21. Економічна постановка та математична модель задачі лінійного програмування. Основні поняття задачі лінійного програмування
- •22. Загальна постановка задачі лінійного програмування. Приклади економічних задач лінійного програмування. Навести відповідні формули.
- •24. Геометрична інтерпретація задач лінійного програмування. Властивості розв’язків задачі лінійного програмування Геометрична інтерпретація задачі лінійного програмування
- •25 Алгоритм графічного методу розв’язування задач лінійного програмування
- •27.Умова оптимальності розв’язку задачі лінійного програмування симплекс-методом. Алгоритм симплексного методу. Навести відповідні формули Оптимальний розв’язок. Критерій оптимальності плану
- •28 Метод штучного базису. Ознака оптимальності плану із штучним базисом. Навести відповідні формули Метод штучного базису (самостійна робота)
- •29 Алгоритм розв’язання розширеної задачі лінійного програмування. Навести відповідні формули
- •31. Двоїста задача. Правила побудови двоїстої задачі. Симетричні й несиметричні двоїсті задачі. Навести відповідні формули
- •32. Економічна інтерпретація прямої задачі лінійного програмування. Економічний зміст двоїстої задачі й двоїстих оцінок
- •33. Перша теорема двоїстості, її економічна інтерпретація. Навести відповідні формули
- •35.Застосування теорем двоїстості в розв’язуванні задач лінійного програмування. Навести відповідні формули см вопр 33,34.
- •37. Аналіз розв’язків лінійних економіко-математичних моделей
- •Основні властивості розв’язків задачі лінійного програмування
- •38. Оцінка рентабельності продукції. Доцільність введення нової продукції. Навести відповідні формули
- •42.Цілочислове програмування. Приклади застосування цілочислових задач в плануванні й управлінні виробництвом. Навести відповідні формули.
- •43. Геометрична інтерпретація задачі цілочислового програмування
- •44.Загальна характеристика методів розв’язування задач цілочислового програмування
- •46. Методи відтинання. Метод Гоморі. Навести відповідні формули.
- •47. Комбінаторні методи. Метод гілок і меж. Навести відповідні формули.
- •48. Наближені методи розв’язання задачі цілочислового лінійного програмування. Метод вектора спаду.
- •49. Постановка задачі нелінійного програмування, математична модель. Геометрична інтерпретація.
- •50.Графічний метод розв’язування задач нелінійного програмування.
- •51. Основні труднощі розв’язування задач нелінійного програмування
- •52. Алгоритм розв’язування задачі на безумовний екстремум. Визначення типу екстремуму. Навести відповідні формули.
- •53. Метод множників Лагранжа пошуку умовного екстремуму функції. Економічна інтерпретація множників Лагранжа. Навести відповідні формули.
- •54. Визначення типу екстремуму. Матриця Гессе. Навести відповідні формули.
- •55. Сідлова точка та необхідні умови її існування. Навести відповідні формули.
- •56. Визначення опуклої та угнутої функції. Теорема Куна-Таккера. Навести відповідні формули.
- •Теорема Куна-Таккера
- •57. Необхідні та достатні умови існування оптимального плану задачі опуклого програмування.
- •58. Квадратична форма та її властивості.
- •59. Постановка задачі квадратичного програмування та її математична модель.
- •60 Метод розв’язування задач квадратичного програмування
- •61. Градієнтні методи розв’язання задач нелінійного програмування. Метод Франка-Вульфа розв’язування задачі нелінійного програмування. Навести відповідні формули.
- •62. Загальна постановка задачі динамічного програмування. Умови застосування моделі динамічного програмування.
- •63. Принцип оптимальності Беллмана. Багатокроковий процес прийняття рішень.
- •64. Основні етапи складання математичної моделі задачі динамічного програмування.
- •65 Етапи рішення задачі динамічного програмування
- •66. Загальна математична постановка задачі стохастичного програмування
- •67. Особливості математичної постановки задач стохастичного програмування
- •68 Основні поняття теорії ігор
- •Матричні ігри двох осіб Якщо у грі беруть участь два гравці, то така гра називається парною (грою двох осіб). Часто у грі беруть участь багато сторін.
- •69 Зведення матричної гри до задачі лінійного програмування
68 Основні поняття теорії ігор
Теорія ігор вперше була систематично викладена Нейманом і Моргенштерном та оприлюднена лише 1944 року в монографії «Теорія ігор і економічної поведінки», хоча окремі результати були опубліковані ще в 20-х роках. Нейман і Моргенштерн написали оригінальну книгу, яка містила переважно економічні приклади, оскільки економічні задачі простіше за інші описати за допомогою чисел.
Розглянемо ситуацію з кількома учасниками, коли значення цільової функції для кожного учасника залежить не лише від його власної поведінки, але і від дій інших суб’єктів.
За умов ринкової економіки все частіше мають місце конфліктні ситуації, коли два або більше колективів (індивідуумів) мають протилежні цілі та інтереси, причому результат дії кожної із сторін залежить і від дії супротивника. Класичним прикладом конфліктної ситуації в економіці є відношення продавець – покупець (монополія – монопсонія). Складніші ситуації виникають, коли в суперечці інтересів беруть участь об’єднання чи коаліції.
Зазначимо, що не завжди учасники ігрової ситуації мають протилежні цілі. Наприклад, дві фірми, які надають однакові послуги, можуть об’єднуватися з метою спільного протистояння більшому супернику.
Часто однією із сторін конфлікту є природні процеси чи явища, наприклад, погода, тобто маємо гру людини з природою. Погодними умовами людина практично не може керувати, але вона має змогу пристосовуватися до її постійних змін. Безліч подібних ситуацій можна зустріти і в інших сферах людської діяльності: біології, психології, політології тощо.
Теорія ігор – це математичний апарат, що розглядає конфлікт ні ситуації, а також ситуації спільних дій кількох учасників. Завдання теорії ігор полягає у розробленні рекомендацій щодо раціональної поведінки учасників гри.
Реальні конфліктні ситуації досить складні і обтяжені великою кількістю несуттєвих чинників, що ускладнює їх аналіз, тому на практиці будують спрощені моделі конфліктних ситуацій, які називають іграми.
Характерними рисами математичної моделі ігрової ситуації є наявність, по-перше, кількох учасників, яких називають гравцями, по-друге, опису можливих дій кожної із сторін, що називаються стратегіями, по-третє, визначених результатів дій для кожного гравця, що подаються функціями виграшу. Задачею кож ного гравця є знаходження оптимальної стратегії, яка за умови багатократного повторення гри забезпечує даному гравцю максимально можливий середній виграш.
Матричні ігри двох осіб Якщо у грі беруть участь два гравці, то така гра називається парною (грою двох осіб). Часто у грі беруть участь багато сторін.
Залежно від кількості стратегій розрізняють скінченні та нескінченні ігри. Якщо кожен гравець має скінченну кількість стратегій, то гра – скінченна, в іншому разі – нескінченна.
Якщо виграш одного гравця дорівнює програшу іншого, то маємо гру з нульовою сумою. Такі ігри характеризуються протилежними інтересами сторін, тобто ситуацією конфлікту. Інші ігри – з ненульовою сумою, виникають як за умов конфліктної поведінки гравців, так і за їх узгоджених дій.
За можливості поєднання інтересів гравців та домовленості між ними про вибір стратегій можна казати про кооперативну гру, коли ж гравці не мають можливості чи не бажають координувати свої дії, то гра називається некооперативною.
Найчастіше розглядається гра з двома гравцями, в яких виграші однієї сторони дорівнюють програшу іншої, а сума виграшів обох сторін дорівнює нулю, що в теорії ігор називають грою двох осіб з нульовою сумою. Ці ситуації є типовими у практичній діяльності менеджерів, маркетологів, спеціалістів рекламних служб, які щоденно приймають рішення в умовах гострої конкуренції, неповноти інформації тощо. Основною метою розв’язування задач цього класу є розробка рекомендацій щодо вибору оптимальних стратегій дії конфліктуючих сторін із застосуванням методичних підходів теорії ігор.
Отже, маємо два гравці А і В (гра двох осіб з нульовою сумою). Кожний гравець обирає одну з можливих стратегій:
гравець
А – стратегії
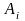 ,
гравець В – стратегії
,
гравець В – стратегії
 .
.
Результати (плата) за всіма можливими варіантами гри задаються, як правило, спеціальними функціями (що залежать від стратегій гравців) у вигляді платіжної матриці.
Нехай
 (Аі;
Вj) –
виграш гравця А,
(Аі;
Вj) –
виграш гравця А,
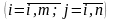 ;
;
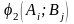 –
виграш
гравця В,
–
виграш
гравця В,
.
Оскільки
гра з нульовою сумою, то
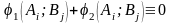 .
.
Тоді
в разі
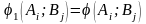 маємо
маємо
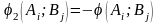 .
.
Отже,
мета гравця А максимізувати
 ,
а гравця В – її мінімізувати. Нехай
,
а гравця В – її мінімізувати. Нехай
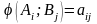 ,
тобто маємо матрицю
,
тобто маємо матрицю

рядки якої відповідають стратегіям Аі, а стовпці – стратегіям Вj.
Матриця А називається платіжною, а також матрицею гри. Елемент цієї матриці aij – виграш гравця А, якщо він вибрав стратегію Ai, а гравець В – стратегію Bj.
Із багатьох критеріїв, які пропонуються теорією гри для вибору раціональних варіантів рішень, найпоширенішим (песимістичним) є критерій мінімаксу-максиміну. Сутність його полягає ось у чому.
Нехай
гравець А вибрав стратегію Аі.
Тоді в найгіршому випадку він отримає
виграш, що дорівнює
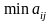 .
Якщо навіть гравець
В знає його стратегію, гравець А має
діяти так, щоб максимізувати свій
мінімальний виграш:
.
Якщо навіть гравець
В знає його стратегію, гравець А має
діяти так, щоб максимізувати свій
мінімальний виграш:
 .
.
Таку стратегію гравця А називають максимінною, а розмір його гарантованого виграшу – нижньою ціною гри.
Стратегія,
яка забезпечує цей виграш, називається
максимінною
і позначається
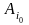 .
.
Гравець
В, який програє суми в розмірі елементів
платіжної матриці, навпаки, має обрати
стратегію, що мінімізує його максимально
можливий програш за всіма варіантами
дій гравця А. Стратегію гравця В називають
мінімаксною
і позначають
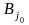 .
Розмір його програшу – верхня
ціна гри:
.
Розмір його програшу – верхня
ціна гри:
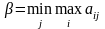 .
.
Оптимальний розв’язок цієї задачі досягається тоді, коли жодній стороні не вигідно змінювати обрану стратегію, оскільки суперник може у відповідь обрати іншу стратегію, яка дасть йому кращий результат. Якщо
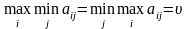 ,
,
тобто
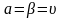 ,
то гра називається цілком
визначеною.
Цілком визначені ігри називаються
іграми
із сідловою точкою.
У цій ситуації оптимальним для обох
гравців є вибір чистих стратегій –
максимінної для гравця А і мінімаксної
для В. Адже, якщо один із гравців додержує
оптимальної стратегії, то для іншого
відхилення від його оптимальної
стратегії не може бути вигідним. Якщо
гра не має сідлової точки, тобто
,
то гра називається цілком
визначеною.
Цілком визначені ігри називаються
іграми
із сідловою точкою.
У цій ситуації оптимальним для обох
гравців є вибір чистих стратегій –
максимінної для гравця А і мінімаксної
для В. Адже, якщо один із гравців додержує
оптимальної стратегії, то для іншого
відхилення від його оптимальної
стратегії не може бути вигідним. Якщо
гра не має сідлової точки, тобто
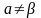 і
і
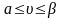 ,
то максимінно-мінімаксні стратегії не
є оптимальними: кожна зі сторін може
поліпшити свій результат, обираючи
інший підхід. Оптимальний розв’язок
такої гри знаходять, застосовуючи
змішані
стратегії,
які є певними комбінаціями початкових
чистих стратегій.
,
то максимінно-мінімаксні стратегії не
є оптимальними: кожна зі сторін може
поліпшити свій результат, обираючи
інший підхід. Оптимальний розв’язок
такої гри знаходять, застосовуючи
змішані
стратегії,
які є певними комбінаціями початкових
чистих стратегій.
Імовірності (або частоти) вибору кожної стратегії задаються відповідними векторами.
Для
гравця А:
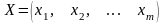 ,
,
де
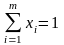 ;
;
Для
гравця В:
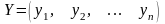 ,
,
де
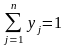 .
.
Очевидно,
що
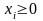 ,
;
,
;
 ,
.
,
.
Розглянемо гру, в якій є сідлова точка.
Маємо гру гравців А і В, яка задана платіжною матрицею. Визначити ціну гри та оптимальні стратегії дій гравців А і В. Оптимізацію гри починають, як правило, визначенням домінуючих стратегій для кожної зі сторін, а також відкиданням невигідних і дублюючих стратегій.
За умови існування такої матриці розв’язок задачі – сідлову точку, ціну та оптимальні стратегії гри – можна знайти значно ефективніше:
Гравець A |
Гравець В
|
Розв’язування. Насамперед визначають домінуючу стратегію. Перша стратегія гравця А домінує над третьою, оскільки всі значення його виграшів за будь-яких дій суперника є не гіршими, ніж у разі вибору третьої стратегії, тобто всі елементи першого рядка платіжної матриці не менші за відповідні елементи її третього рядка. Тому третя стратегія гірша за першу й може бути вилучена з платіжної матриці.
Аналізуючи далі можливі дії гравця B, зауважимо, що його перша стратегія домінує над четвертою, яку можна відкинути як більш збиткову, а тому невигідну для цього гравця. Отже, маємо таку платіжну матрицю:
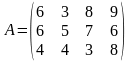 .
.
У
разі вибору гравцем А першої стратегії,
залежно від дій гравця В він може
отримати 6, 3, 8 або 9 одиниць. Але завжди
його
виграш буде не меншим за
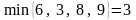 ,
тобто незалежно від поведінки гравця
В. Якщо розглянути можливі наслідки
вибору гравцем А другої стратегії, то
аналогічно його гарантований виграш
становитиме
,
тобто незалежно від поведінки гравця
В. Якщо розглянути можливі наслідки
вибору гравцем А другої стратегії, то
аналогічно його гарантований виграш
становитиме
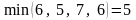 .
Для третьої стратегії відповідно маємо:
.
Для третьої стратегії відповідно маємо:
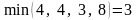 .Отже,
нижня ціна гри:
.Отже,
нижня ціна гри:
 ,
а гравець А для максимізації мінімального
виграшу має обрати другу з трьох можливих
стратегій. Така стратегія є максимінною
в цій грі.
,
а гравець А для максимізації мінімального
виграшу має обрати другу з трьох можливих
стратегій. Така стратегія є максимінною
в цій грі.
Гравець
В, який намагається мінімізувати свій
програш, обираючи першу стратегію, може
програти 6,6 або 4 одиниці. Але за будь-яких
варіантів дій гравця А він може програти
не більш як
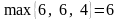 .
Для другої стратегії маємо
.
Для другої стратегії маємо
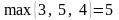 ,
для третьої –
,
для третьої –
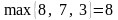 ,
для четвертої –
,
для четвертої –
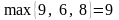 .
Отже, верхня ціна гри
.
Отже, верхня ціна гри
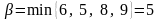 .
.
І гравцю В доцільно вибирати другу стратегію, яка є мінімаксною у грі.
Оскільки
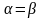 ,
ця гра має сідлову точку, ціна гри
дорівнює 5. Оптимальною максимінною
стратегією гравця А є друга з трьох
можливих стратегій його дій. Для гравця
В оптимальною є також друга з чотирьох
можливих.
,
ця гра має сідлову точку, ціна гри
дорівнює 5. Оптимальною максимінною
стратегією гравця А є друга з трьох
можливих стратегій його дій. Для гравця
В оптимальною є також друга з чотирьох
можливих.