54. Визначення типу екстремуму. Матриця Гессе. Навести відповідні формули.

Узагальнення достатньої умови існування локального екстремуму для функції n змінних приводить до такого правила: за функ­цією Лагранжа виду (8.8) будується матриця Гессе, що має блочну структуру розмірністю :

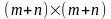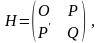
де О – матриця розмірністю , що складається з нульових елементів,

Р – матриця розмірністю 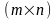, елементи якої визначаються так:

,

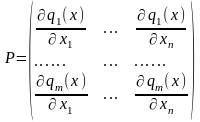– транспонована матриця до Р розмірністю ,

Q – матриця розмірністю 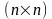виду:

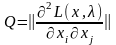, де .

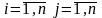Розглянемо ознаки виду екстремуму розв’язку системи (8.9). Нехай стаціонарна точка має координати і .

1. Точка 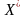є точкою максимуму, якщо, починаючи з голов­ного мінору порядку (m+1), наступні (n–m) головних мінорів матриці Н утворюють знакозмінний числовий ряд, знак першого члена якого визначається множником .

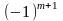2. Точка є точкою мінімуму, якщо, починаючи з головного мінору порядку (m+1), знак наступних (n–m) головних мінорів матриці Н визначається множником .

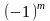55. Сідлова точка та необхідні умови її існування. Навести відповідні формули.

Для розроблення методів розв’язування окремих типів задач нелінійного програмування важливе значення має поняття сідлової точки, а також визначення необхідних і достатніх умов існування сідлових точок функції Лагранжа 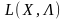у (n+m)-вимірному просторі змінних 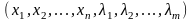за довільних умов, які можуть накладатися на їх знаки (необхідні і достатні умови існування сідлової точки функції Лагранжа за відсутності обмежень на знаки змінних розглянуто в п.8.4).

Розглянемо нелінійну задачу:

,

.

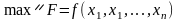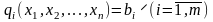Причому на компоненти векторів 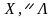накладено обмеження на знаки. Позначимо множину точок, що задовольняють такі обмеження, через .

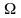Функція Лагранжа для цієї задачі має вигляд:

= .(8.12)

Точка 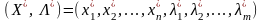називається сідловою точкою функції Лагранжа (8.12), якщо для всіх 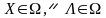виконується співвідношення:

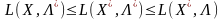.(8.13)

Для диференційовних функцій 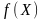та 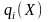знайдемо необхідні умови існування сідлової точки.

Сідлова точка 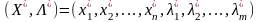функції виду (8.12) за означенням задовольняє умову:

.

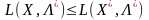Нерівність виконується для всіх точок Х, тобто також і для тих, у яких лише одна координата відрізняється від Х^*. Допустимо, що це х_k, а всі інші збігаються з координатами сідлової точки .

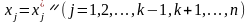Оскільки права частина нерівності є фіксованою, а в лівій частині змінюється лише одна координата х_k, то приходимо до функ­ції однієї змінної 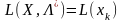, яку можна зобразити графічно на координатній площині.

Розглянемо спочатку випадок, коли 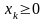, тобто лише частину координатної площини, для якої .

Можливі такі випадки:

1) коли всі , то максимальне значення функції L(x_k) досягатиметься в точці, для якої 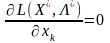(рис.8.5).

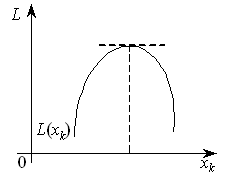
Рисунок 8.5

2) коли максимум функції L(x_k) досягатиметься в точці 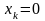і розглядувана частинна похідна також дорівнюватиме нулю: (рис.8.6).

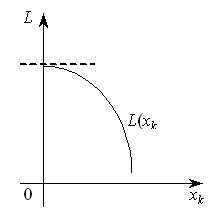
Рисунок 8.6

3) коли точка максимуму функції L(x_k) досягатиметься також у точці , а частинна похідна 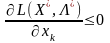(рис.8.7).

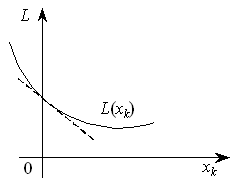
Рисунок 8.7

Узагальнюючи всі три ситуації, маємо:

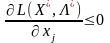для

та

.

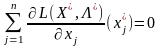Розглядаючи другу частину нерівності (8.13):

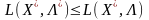
аналогічними міркуваннями, що проілюстровані рис.8.8-8.9, встановлюються необхідні умови для похідних по 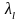функції Лагранжа в сідловій точці.

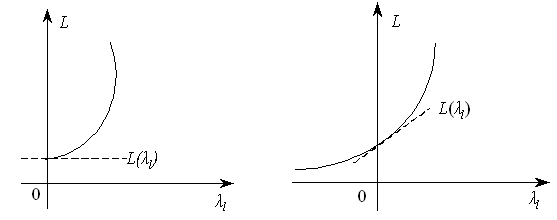
Рисунок 8.8 Рисунок 8.9

Об’єднуючи всі три випадки для невід’ємних координат, маємо необхідні умови сідлової точки:

для тих індексів j, де .(8.14)

Зауважимо, що для маємо ті самі випадки, які зображено на рис.8.5-8.9, причому графіки будуть симетрично відоб­ражені відносно осі Оy, тобто для недодатних координат необхідна умова має вигляд:

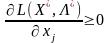для тих індексів j, де .(8.15)

І нарешті, як відомо з попереднього параграфа, якщо на знак х_j умови не накладаються, то необхідною умовою є:

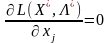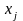, – довільного знака. (8.16)

Узагальнення всіх випадків приводить до рівняння:

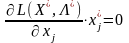.(8.17)

Розглядаючи другу частину нерівності (8.13), за допомогою аналогічних міркувань встановлюємо необхідні умови для похідних по функції Лагранжа в сідловій точці:

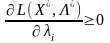для тих індексів і, де 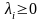,(8.18)

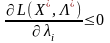для тих індексів і, де 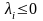,(8.19)

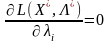для тих індексів і, де має довільний знак.(8.20)

Отже, справджується рівняння:

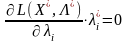.(8.21)

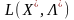Сукупність співвідношень (8.14)-(8.21) становить необхідні умови, які має задовольняти сідлова точка функції Лагранжа для точок, що належать множині . При цьому повинна мати частинні похідні по всіх компонентах векторів .
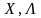