52. Алгоритм розв’язування задачі на безумовний екстремум. Визначення типу екстремуму. Навести відповідні формули.

У теорії дослідження функцій задача на відшукання екстремальних значень не містить ніяких додаткових умов щодо змінних і такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.

Нагадаємо, що необхідна умова існування локального екстремуму функції двох змінних формулюється так: для того, щоб точ­ка 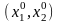була точкою локального екстремуму, необхідно, щоб функція 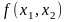була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними 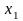та у цій точ­ці дорівнювали нулю:

.

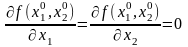Точка називається критичною.

Достатня умова існування локального екстремуму функції двох змінних формулюється так: для того, щоб критична точка була точкою локального екстремуму, достатньо, щоб функ­ція була визначена в околі критичної точки та мала в цій точці неперервні частинні похідні другого порядку.

Тоді, якщо

,

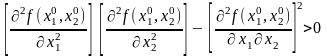то в точці функція має екстремум, причому, якщо

,

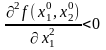тоді – точка локального максимуму функції , а якщо

,

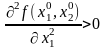тоді – точка локального мінімуму функції .

У разі, якщо

,

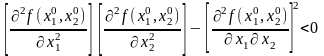то в точці функція екстремуму не має.

Якщо

,

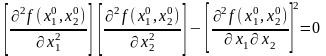то питання про існування екстремуму залишається відкритим.

53. Метод множників Лагранжа пошуку умовного екстремуму функції. Економічна інтерпретація множників Лагранжа. Навести відповідні формули.

Якщо задача полягає у відшуканні локального чи глобального екстремуму деякої функції за умови, що на змінні такої функції накладаються додаткові обмеження, то маємо задачу пошуку умовного екстремуму функції. Термін «умовний» означає, що змінні задачі мають задовольняти деякі умови.

Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення подальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних.

Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:

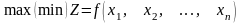(8.6)

за умов:

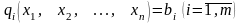,(8.7)

де функції і 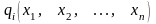мають бути диференційовними.

Задача (8.6)-(8.7) полягає в знаходженні екстремуму функції 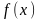за умов виконання обмежень .

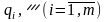Переходимо до задачі пошуку безумовного екстремуму. Теоретично доведено, що постановки та розв’язання таких задач еквівалентні.

Замінюємо цільову функцію (8.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:

(8.8)

де 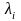– деякі невідомі величини, що називаються множниками Лагранжа.

Знайдемо частинні похідні і прирівняємо їх до нуля:

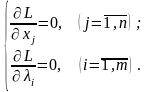
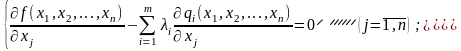(8.9)

Друга група рівнянь системи (8.9) забезпечує виконання умов (8.7) початкової задачі нелінійного програмування.

Система (8.9), як правило, нелінійна.

Розв’язками її є 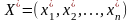і – стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (8.6)-(8.7) або можуть бути точками перегину (сідловими точками).

Для діагностування стаціонарних точок і визначення типу екст­ремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій 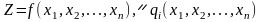існують другі частинні похідні і вони неперервні).