43. Геометрична інтерпретація задачі цілочислового програмування

Д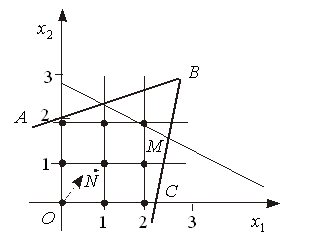 ля знаходження оптим-го розв’язку цілочислових задач застосовують спец. методи. Найпростішим з них є знаходження оптим-го розв’язку задачі як такої, що має лише неперервні змінні, з подальшим їх округленням. Такий підхід є виправданим тоді, коли змінні в оптимальному плані набувають досить великих значень у зіставленні їх з одиницями вимірювання. Проте за деяких умов такі округлення призводять до істотних неточностей. Скажімо, множина допустимих розв’язків деякої нецілочислової ЗЛП має вигляд, зображений на рис. 6.1: Макс. значення функціонала для даної задачі знаходиться в точці В. Округлення дасть таке значення оптимального плану х1=3;х2=3 (точка D на рис.1). Очевидно, що т. D не може бути розв’язком задачі, оскільки вона не належить множині допустимих розв’язків (площ. ОАВС), тобто відповідні значення змінних не задовольнятимуть систему обмежень задачі. Зауважимо, що геометрично множина допустимих планів будь-якої лінійної цілочислової задачі являє собою систему точок з цілочисловими координатами, що знаходяться всередині опуклого багатокутника допустимих розв’язків відповідної нецілочислової задачі. Отже, для розглянутого на рис. 6.1 випадку множина допустимих планів складається з 9 точок (рис. 2), які утворені перетинами сім’ї прямих, що паралельні осям Ох1 та Oх2 і проходять через точки з цілими координатами 0, 1, 2. Для знаходження цілочислового оптимального розв’язку пряму, що відповідає цільовій функції, пересуваємо у напрямку вектора нормалі N до перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і є оптим-им цілочисловим розв’язком задачі. У прикладі оптим-ий цілочисловий розв’язок відповідає т.М (х1=2;х2=2). Особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною ЗЛП полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної ЗЛП є опуклий багатогранник, а вимога цілочисловості розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок. Якщо у разі 2 змінних розв’язок задачі можна відшукати графічним методом, тобто, використовуючи цілочислову сітку, можна досить просто знайти оптим-ий план, то в ін. разі необхідно застосовувати спец. методи.

44.Загальна характеристика методів розв’язування задач цілочислового програмування

Для знаходження оптимальних планів задач цілочислового програмування застосовують такі групи методів:

1) точні методи:

• методи відтинання;

• комбінаторні методи;

2) наближені методи.

Основою методів відтинання є ідея поступового «звуження» області допустимих розв’язків розглядуваної задачі. Пошук цілочислового оптимуму починається з розв’язування задачі з так званими послабленими обмеженнями, тобто без урахування вимог цілочисловості змінних. Далі введенням у модель спеціальних додаткових обмежень, що враховують цілочисловість змінних, багатогранник допустимих розв’язків послабленої задачі поступово зменшують доти, доки змінні оптимального розв’язку не набудуть цілочислових значень.

До цієї групи належать:

а) методи розв’язування повністю цілочислових задач (дробовий алгоритм Гоморі);

б) методи розв’язування частково цілочислових задач (другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).

Комбінаторні методи цілочислової оптимізації базуються на ідеї перебору всіх допустимих цілочислових розв’язків, однак, згідно з їх процедурою здійснюється цілеспрямований перебір лише досить невеликої частини розв’язків.

Найпоширенішим у цій групі методів є метод гілок і меж.

Починаючи з розв’язування послабленої задачі, він передбачає поділ початкової задачі на дві підзадачі через виключення областей, що не мають цілочислових розв’язків, і дослідження кожної окремої частини багатогранника допустимих розв’язків.

Д ля розв’язування задач із бульовими змінними застосовують комбінаторні методи, причому, оскільки змінні є бульовими, то методи пошуку оптимуму значно спрощуються.

Досить поширеними є також наближені методи розв’язування цілочислових задач лінійного програмування. Оскільки для практичних задач великої розмірності за допомогою точних методів не завжди можна знайти строго оптимальний розв’язок за прий­нятний час або для розв’язування задачі використовуються наближено визначені, неточні початкові дані, то часто в реальних задачах досить обмежитися наближеним розв’язком, пошук якого є спрощеним.

Значна частина наближених алгоритмів базується на використанні обчислювальних схем відомих точних методів, таких, наприклад, як метод гілок і меж.

До наближених методів належать: метод локальної оптимізації (метод вектора спаду); модифікації точних методів; методи випадкового пошуку та ін.

Головними показниками для зіставлення ефективності застосування конкретних наближених алгоритмів на практиці є такі: абсолютна 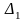та відносна 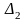похибки отриманих наближених розв’язків.

∆₁=F(X^*)-F(X₁)

∆₂=| F(X^*)-F(X₁)|/|F(X^*)|

де F — цільова функція (в даному разі для визначеності допускаємо вимогу відшукання максимального її значення); Х₁— наближений розв’язок, знайдений деяким наближеним методом; Х^* — оптимальний план задачі.

45. Задача математичного програмування, змінні якої мають набувати цілих значень, називається задачею цілочислового програмування. У тому разі, коли цілочислових значень мають набувати не всі, а одна чи кілька змінних, задача називається частково цілочисловою.

До цілочислового програмування належать також ті задачі оптимізації, в яких змінні набувають лише двох значень: 0 або 1 (бульові, або бінарні змінні).

Геометрично множина допустимих планів будь-якої лінійної цілочислової задачі являє собою систему точок з цілочисловими координатами, що знаходяться всередині опуклого багатокутника допустимих розв’язків відповідної нецілочислової задачі. Отже множина допустимих планів складається з дев’яти точок (рис.7.2), які утворені перетинами сім’ї прямих, що паралельні осям Ох₁ та Oх₂ і проходять через точки з цілими координатами 0, 1, 2.

Рисунок 7.2

Для знаходження цілочислового оптимального розв’язку пряму, що відповідає цільовій функції, пересуваємо у напрямку вектора нормалі до перетину з кутовою точкою утвореної цілочислової сітки. Координати цієї точки і є оптимальним цілочисловим розв’язком задачі. У нашому прикладі оптимальний цілочисловий розв’я­зок відповідає точці М (x1=2;x2=2).

Очевидно, особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисловості розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок. Якщо у разі двох змінних розв’язок задачі можна відшукати графічним методом, тобто, використовуючи цілочислову сітку, можна досить просто знайти оптимальний план, то в іншому разі необхідно застосовувати спеціальні методи.