38. Оцінка рентабельності продукції. Доцільність введення нової продукції. Навести відповідні формули

Оцінку рентабельності продукції, що виготовляється на підприємстві, можна здійснювати за допомогою двоїстих оцінок та обмежень двоїстої задачі, які характеризують кожний вид продукції.

Л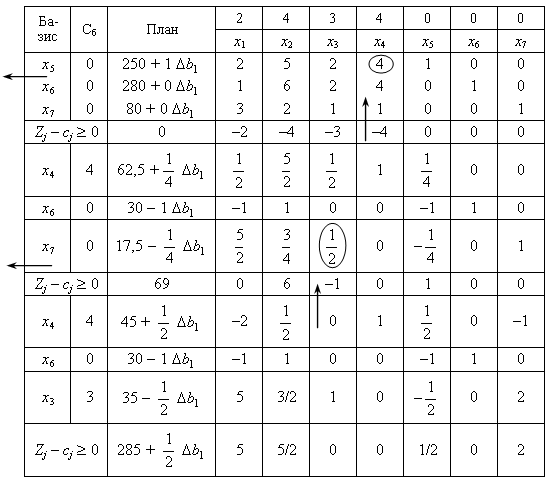 іва частина кожного обмеження двоїстої задачі є вартістю відповідних ресурсів, які використовують для виробництва одиниці j-ї продукції. Якщо ця величина перевищує ціну одиниці продукції (с_j), то вона нерентабельна і в оптимальному плані прямої задачі відповідна їй змінна х_j = 0. Якщо ж загальна оцінка всіх ресурсів дорівнює ціні одиниці продукції, то виготовляти таку продукцію доцільно, вона рентабельна і в оптимальному плані прямої задачі відповідна змінна х_j > 0.

значення додаткових змінних оптимального плану двоїстої задачі показують, наскільки вартість ресурсів перевищує ціну одиниці відповідної продукції. Тому, якщо додаткова змінна двоїстої задачі дорівнює нулю, то продукція рентабельна. І, навпаки, якщо у_і > 0, то відповідна продукція нерентабельна.

Оптимальні значення у₄ = 5 > 0; у₅ = 5/2 > 0, тому продукція А і В нерентабельна, а у₆ = 0; у₇ = 0, тобто продукція С і D — рентабельна.

Дослідимо питання про доцільність введення нового (n + 1)-го виду продукції, якщо відомі витрати кожного ресурсу на виготов­лення одиниці такої продукції —a_i,n+1 (i=1,m)і ціна її реалізації — с_n+1. За умови введення у виробництво нового виду продук­ції в економіко-математичну модель необхідно ввести відповідну змінну (х_n+1). Отже, модель прямої задачі набуде вигляду:

max Z= с₁х₁ + с₂х₂ + … + с_nx_n+ с_n+1x_n+1

за умов:

а₁₁х₁+а₁₂х₂…+а_1nx_n+a₁,_n+1x_n+1 ≤b₁

а₂₁х₁+а₂₂х₂…+а_2nx_n a₂,_n+1x_n+1 ≤b₂

… (2.2)

а_m1х₁+а_m2х₂…+а_mnx_n+a_m,_n+1x_n+1 ≤b_m

x_j≥0; …j=1,n

Відповідна математична модель двоїстої задачі міститиме не n, а (n + 1) нерівність і відрізнятиметься наявністю обмеження, що описує витрати на виробництво нового виду продукції: a_1.n+1y₁+a_2,n+1y_2+…+ a_m,_n+1y_m≥c_n+1

Оскільки значення a_i,n+1 (i=1,m) і с_n+1 за умовою задачі відомі, розраховані також значення y_i (i=1,m), то можна перевірити виконання нерівності. Як зазначено вище, рентабельною є продукція, для якої відповідне обмеження виконується як рівняння, а нерентабельною, якщо ліва частина нерівності (витрати на вир-во) перевищує праву (ціну реалізації).

39. Аналіз обмежень дефіцитних і недефіцитних ресурсів. Інтервали можливої зміни обсягів дефіцитних ресурсів. Дослідження взаємозамінювання ресурсів

За допомогою двоїстих оцінок можна визначити статус кожного ресурсу (дефіцитні та недефіцитні залежно від того, повне чи часткове їх використання передбачене оптимальним планом прямої задачі). Якщо деяке значення двоїстої оцінки в оптимальному плані двоїстої задачі у_і=0, то відповідний і-й ресурс використов у вир-ві продукції не повністю і є недефіцитним. Якщо ж двоїста оцінка у_і > 0, то і-й ресурс використ повністю і називається дефіцитним. Відомо (третя теорема двоїстості), що величина двоїстої оцінки показує, наскільки збільшиться значення ЦФ Z, якщо запас відповідного ресурсу збільшити на одну умовну одиницю.

Існує 3 способи дослідження статусу ресурсів: 1 — підстановкою значень вектора Х* (оптимального плану виробництва) у систему обмежень прямої задачі. Якщо обмеження виконується як рівняння, то відповідний ресурс дефіцитний, у іншому разі — недефіцитний:.

2. Додаткові змінні в оптим плані прямої задачі економічно означають залишки відповідних ресурсів і тому, якщо додаткова змінна в оптим плані прямої задачі = 0, то такий ресурс є дефіцитним, а якщо быльша від нуля — недефіцитний.

3. за допомогою двоїстих оцінок. Якщо у_і > 0, то зміна (збільшення або зменшення) обсягів і-го ресурсу приводить до відповідної зміни доходу підприємства, і тому такий ресурс є дефіцитним. Якщо ж у_і = 0, то і-й ресурс недефіцитний.

Щоб для розрахувати інтервали можливої зміни обсягів дефіцитних ресурсів, у межах яких двоїсті оцінки у_і залишаються на рівні оптимальних значень, тобто розв’язати систему нерівностей

Якщо приріст (зміну) запасу першого ресурсу позначимо через b₁, тоді симплексні таблиці даної задачі набудуть вигляду:

Новий оптимальний план можна записати у такий спосіб:

Х^* = (0; 0; 35–1/2b₁; 45 + 1/2b₁; 0; 30 – b₁; 0).

Єдина вимога, яку можна поставити до можливих нових оптимальних значень, – це умова невід’ємності змінних, тобто:

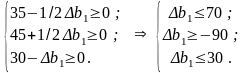
Отже,-90≤∆b₁≤30

Це означає, що коли запас ресурсу 1 збільшиться на 30 ум.од. або зменшиться на 90 ум. од., то на цьому інтервалі його оптимальна двоїста оцінка залишиться такою ж: у₁=1/2. Отже, запас ресурсу 1 може змінюватись у межах: 250-90≤∆b₁≤250+30 160≤∆b₁≤280

Згідно з цим максимально можливі зміни обсягів виручки підприємства залежно від змін у постачанні ресурсу 1 на такому інтервалі будуть у межах:

285-90*1/2≤Z_max≤285+30*1/2 240≤Z_max≤300, а відповідні критичним значенням діапазону виручки оптимальні плани виробництва продукції будуть такими:(0; 0; 80; 0; 0; 120; 0) = Х^* = (0; 0; 20; 60; 0; 0; 0).

Аналогічно розраховується інтервал стійкості двоїстої оцінки у₃ = 2 для дефіцитного ресурсу 3:

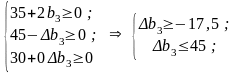
-17,5≤∆b₃ ≤45, 62,5 ≤b₃ ≤125

Отже, якщо запас ресурсу 3 збільшиться на 45 ум.од. або змен­шиться на 17,5 ум.од., то двоїста оцінка у₃=2 цього ресурсу залишиться такою ж. Згідно із цим можлива виручка підприємства та оптимальний план виробництва продукції будуть знаходитися у межах: 250≤Z_max≤375

(0; 0; 0; 62,5; 0; 30; 0) = Х* = (0; 0; 125; 0; 0; 30; 0).

Для розрахунку інтервалу зміни недефіцитного ресурсу досить розв’язати одну нерівність .

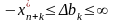У нашому прикладі недефіцитним є другий ресурс. Відомо, що за оптимального плану виробництва буде залишок цього ресурсу в обсязі x₆=30 ум. од. Отже, зменшення даного ресурсу в обсязі до 30 ум. од. не змінить структуру оптимального плану. Якщо зміну загального запасу другого ресурсу позначити через 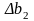, то інтервал можливої зміни його обсягів можна записати так:-30≤∆b₂≤∞.

Отже, інтервалом зміни запасів недефіцитного ресурсу, в межах якого структура оптимального плану залишиться постійною, буде 250≤b₂≤∞

Зауважимо, що визначені інтервали стосуються лише тих випадків, коли змінюється обсяг тільки одного ресурсу, а запаси всіх інших фіксовані, тобто за інших однакових умов. У разі одночасної зміни обсягів усіх або кількох ресурсів для визначення інтервалів допустимих змін необхідно розв’язати систему нерівностей

, .

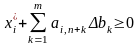40. Аналіз діапазону зміни коефіцієнтів цільової функції задач лінійного програмування. Навести відповідні формули.

Розглянемо задачу лінійного програмування Допустимо, що коефіцієнт цільової функції при деякій k-ій змінній 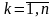з початковим значенням 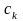змінився на величину 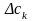. Отже, цільова функція набуде вигляд у: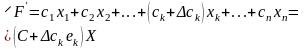 (3.49)

де С, Х — відповідно вектор компонент цільової функції та вектор змінних, e_k — одиничний вектор-рядок, де одиниця відповідає k-ій компоненті.

визначення границь можливих змін коефіцієнтів цільової функції, в межах яких структура оптимального плану залишається постійною.

А. Перший випадок — коефіцієнт c_k відповідає базисній змінній оптимального плану. За припущенням базисними змінними оптимального плану є перші m векторів останньої симплексної таблиці, отже, .

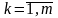Зміни коефіцієнтів цільової функції в процесі реалізації симплексного методу впливатимуть лише на значення оцінкового ряду ( ).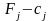

Для оптимального плану задачі (3.36)—(3.38), , оцінки векторів розраховують так:

.

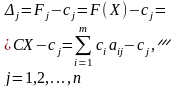Якщо цільова функція має вигляд 3.49, то оцінки векторів розраховуватимуться за формулою:

,

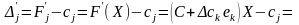
де а_kj — елементи вектора-рядка, який є результатом множення e_k на Х.

В. Другий випадок — змінюється коефіцієнт цільової функції при небазисній змінній.

Зміна коефіцієнта цільової функції небазисної змінної впливає на оцінку лише цієї змінної. Допустимо, що це коефіцієнт Ск і за припущенням у даній задачі

Нехай цей коефіцієнт зміниться на величину . Тоді для задачі з цільовою функцією (3.49) в останній симплексній таблиці зміниться лише одна оцінка, що відповідає небазисній змінній Хк.

Де дельта К - оцінка вектора при змінній задачі (3.36)—(3.38). Дана оцінка має бути невід’ємною, отже:

Для небазисної змінної діапазон стійкості оптимального плану визначається нерівністю:

Тобто для коефіцієнтів цільової функції при небазисних змінних існує лише верхня межа зміни діапазон

С. Якщо коефіцієнти при змінних цільової функції (3.36) задачі лінійного програмування водночас змінюються для кількох чи всіх значень то визначення границь можливих змін величин здійснюється аналогічно випадку (А).

Для того, щоб план задачі з цільовою функцією, в якій одночасно змінюються кілька чи всі значення та системою обмежень (3.37), (3.38) також був оптимальним, має виконуватися умова, аналогічна (3.50)

41. Аналіз діапазону зміни компонент вектора обмежень задач лінійного програмування. Навести відповідні формули.

Допустимо, що деяке k-те обмеження має в правій частині початкове значення Bk

Нехай початкова величина змінилась на величину .Отже, k-те обмеження в системі (3.37) буде мати вигляд:

Для зведення (3.39) до канонічного виду необхідно ввести додаткову змінну xn+k (якщо обмеження має вигляд рівняння, то як таку змінну можна розглядати невід’ємну штучну змінну).

А. Розглянемо випадок, коли додаткова змінна в оптимальному плані небазисна і дорівнює нулю.

З першої теореми двоїстості відомо, що оптимальний план прямої задачі (як і кожен поточний опорний план) можна подати у вигляді: де D — матриця, що складена з компонент векторів А1А2 останнього базису. , — оптимальний план задачі (3.36)—(3.38); В — вектор, що складається з вільних членів системи обмежень в останній симплексній таблиці. Отже, якщо змінюються компоненти вектора В, то змінюються також значення Однак існує діапазон, у межах якого всі компоненти алишаються невід’ємними, тобто структура оптимального плану не змінюється. Визначимо ці межі..Вектор В подамо у вигляд: де ek — одиничний вектор-стовпчик, а в ньому одиниця — k-та компонента. Тоді, використовуючи (3.40), маємо: .де dk — (добуток матриці D–1 на одиничний вектор ek) k-ий стовпчик матриці D–1.

Позначимо елементи k-го стовпчика матриці через ,тоді:

В. Розглянемо випадок, коли додаткова змінна — базисна. Якщо додаткова змінна xn+k базисна, то це означає, що у виразі (3.42) dk –одиничний вектор з k-ою компонентою, рівною одиниці, отже, система нерівностей (3.43) перетвориться в таку:

Очевидно, що значення додаткової базисної змінної визначає діапазон змін, в якому відповідна компонента bk може зменшуватись (збільшуватись для обмежень типу «>»)

Оптимальний план залишається незмінним у діапазоні bk + Δbk для тих , яким відповідають додаткові базисні змінні xn + k, де . для обмежень системи (3.37) типу «>».

Для задачі знаходження мінімального значення цільової функції та обмежень системи (3.37) типу «> » можливі зміни компонент правої частини системи обмежень визначаються з нерівності:

де к=1,m

С. Якщо компоненти вектора вільних членів системи обмежень задачі лінійного програмування змінюються водночас для кількох чи всіх значень то визначення границь можливих змін величин тає надто складною проблемою. Однак у такому разі завжди можна перевірити, чи задовольняють конкретні зміни величин систему виду: ,де Е — одинична матриця. Якщо позначити елементи матриці через тоді:

Оскільки необхідно, щоб план також був оптимальним, має виконуватися умова невід’ємності всіх компонент вектора, отже:

,тобто:

3.47.

Якщо значення задовольняють всі нерівності системи (3.47), то структура оптимального плану задачі (3.36)—(3.38) залишається постійною.

Для визначення верхньої та нижньої границь змін в межах яких структура оптимального плану залишається постійною, необхідно розв’язати систему нерівностей (3.47). Однак у більшості випадків для знаходження оптимального плану нової задачі лінійного програмування ростіше розв’язати задачу симплексним методом, змінюючи вільні члени системи (3.37) на