35.Застосування теорем двоїстості в розв’язуванні задач лінійного програмування. Навести відповідні формули см вопр 33,34.

І т-ма: Якщо одна із спряжених задач має розв’язок то друга задача теж має розв’язок і знач-я цієї ф-ції співпадатимуть. Х^*=(x^*₁,x^*₂,x^*₃…x^*_n);Y^*=(y^*₁,y^*₂,y^*₃…y^*_n); F_max=F(x^*)=>Z_min=Z(y^*);Fmax=Zmin; Max прибуток F підпр-во має від реалізації оптим плану х*, однак ту ж суму він отримає від продажу ресурсів за оптим. Цінами у*. ІІ т-ма: При підстановці оптим плану х^* в і-те обмеж-я прямої задачі можна отримати 2 варіанти оцінки ресурсів, якщо маємо знак (=), то ресурс викор-ся повністю, він є дефіцитним тобто цінним, його треба поповнювати, його двоїста оцінка є додатнім числом. ІІІ т-ма: Компоненти оптим плану Y*i дають оцінку дефіцитних і недефіц-их ресурсів, а кожне додатнє знач-я двоїстої оцінки характер-є приріст цільової ф-ції F, зумовлю-ий малими змінами на одиницю відповідного запасу дефіцитних ресурсів. В симплекс таблиці знач-я двоїстих оцінок знаходь в останньому перевірочному рядку навпроти баз. змінних прямої задачі.

36. Алгоритм рішення задачі лінійного програмування двоїстим симплексним методом

Двоїсту задачу можна також розв’язати за таблицею, в якій записана пряма, а відшукавши оптимальний план двоїстої задачі, разом з тим отримати розв’язок початкової задачі. Такий спосіб розв’язання ЗЛП має назву двоїстого симплексного методу. Прямий та двоїстий симплексні методи пов’язані між собою.

Нехай необхідно розв’язати задачу лінійного програмування, подану в канонічному виді:

minF=CX (3.60)

AX=B (3.61)

X≥0 (3.62)

Тоді двоїстою до неї буде така задача:

maxZ=BY (3.63)

YA≤C (3.64)

За алгоритмом двоїстого симплексного методу:

як перший опор­ний план вибирається деякий допустимий розв’язок двоїстої задачі «псевдоплан») і зберігається його допустимість для двоїстої задачі упродовж всіх кроків.

Допустимо, що початковий базис складається з m векторів D=(A₁,A₂,…,A_m ), причому хоча б одна з компонент вектора X=D^-1 B=(x₁,x₂,…x_l..x_n) від’ємна. Нехай x_l<0, однак всі оцінки векторів ∆_j=F_j-c_j≥0 (j=1,n). На підставі першої теореми двоїстості план двоїстої задачі відшукуємо у вигляді: Y=C_базD^-1. Цей план не є оптимальним для прямої задачі, оскільки він не задовольняє умову невід’ємності змінних і не є оптимальним для двоїстої задачі, бо всі оцінки векторів оптимального плану двоїстої задачі мають бути невід’ємними.

Отже, вектор, що відповідає компоненті x_l<0, потрібно виключити з базису початкової задачі, а вектор двоїстої задачі, що відповідає від’ємній оцінці, включити до базису двоїстої.

У прямому симплекс-методі спочатку виявляють змінну, яку слід ввести у базис, а в двоїстому симплекс-методі навпаки — спочатку визначають змінну, яку виключають з базису, а потім змінну, яку вводять у базис.

Алгоритм двоїстого симплексного методу:

1. Необхідно звести всі обмеження задачі до виду «», ввести додаткові невід’ємні змінні, визначити початковий базис та перший опорний план X=(b₁,b₂…b_m).

2. Якщо всі оцінки векторів ∆_j=F_j-c_j≤0 і компоненти вектора-стовпчика «План» =(b₁,b₂…b_m)≥0 для всіх i=1,m, то задача розв’язана. Інакше необхідно вибрати найбільшу за модулем компоненту b_i<0 і відповідну змінну x_l виключити з базису.

3. Якщо в l-му рядку, що відповідає змінній x_l, не міститься жодного a_ij<0, то ЦФ двоїстої задачі необмежена на багатограннику розв’язків, а початкова задача розв’язку не має. Інакше існують деякі a_ij<0 і тоді для відповідних стовпчиків визначають аналогічно прямому симплекс-методу оцінки Ө:

Ө_j=min |∆_j/a_ij| (a_ij<0), що дає змогу вибрати вектор, який буде включено в базис.

4. Виконавши крок методу повних виключень Жордана—Гаусса, переходять до наступної симплексної таблиці (Переходять до пункту 2).

Зазначимо, що для задачі знаходження максимального значення цільової функції за наведеним алгоритмом необхідно перейти до цільової функції 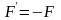, або дещо змінити сам алгоритм.