33. Перша теорема двоїстості, її економічна інтерпретація. Навести відповідні формули

На всякий случай:

Лема1 (основна нерівність теорії двоїстості). Якщо X=(x₁,x₂…x_n) та Y=(y₁,y₂,…y_m) — допустимі розв’язки відповідно прямої та двоїстої задач, то виконується нерівність F(X)≤Z(Y) f,j або ∑ c_jx_j≤∑b_iy_i (j=1,n; i=1,m)

Лема 3.2 (достатня умова оптимальності). Якщо X^*=(x₁^*,x₂^*…x_n^*) та Y^*=(y₁^*,y₂^*,…y_m^*) — допустимі розв’язки відповідно прямої та двоїстої задач, для яких виконується рівність F(X*)=Z(Y*) то X^*, Y^* — оптимальні розв’язки відповідних задач.

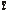Перша теорема двоїстості. Якщо одна з пари двоїстих задач має оптимальний план, то інша задача також має розв’язок, причому значення цільових функцій для оптимальних планів дорівнюють одне одному, тобто max Z = min F, і навпаки.

Якщо ж ЦФ однієї з пари двоїстих задач не обмежена, то друга задача взагалі не має розв’язків.

Якщо пряма ЗЛП має оптимальний план Х ^*, визначений симплекс-методом, то оптимальний план двоїстої задачі Y ^* визначається зі співвідношення У^*=с_баз D^-1

де с_баз — вектор-рядок, що складається з коефіцієнтів ЦФ прямої задачі при змінних, які є базисними в оптимальному плані; D^-1 — матриця, обернена до матриці D, складеної з базисних векторів оптимального плану, компоненти яких узято з початкового опорного плану задачі. Обернена матриця D^-1 завжди міститься в останній симплекс-таблиці в тих стовпчиках, де в першій таблиці містилася одинична матриця.

За допомогою зазначеного співвідношення під час визначення оптимального плану однієї з пари двоїстих задач лінійного програмування знаходять розв’язок іншої задачі.

Ек.зміст теореми: макс.прибуток підпр-во отримує за умови в-ва продукції згідно з оптим.планом Х^*=(x₁^*,x₂^*…x_n^*) , однак таку саму кількість грошей (Z_min=F_max) підпр.може мати, реалізувавши ресурси за оптим.цінами Y^*=(y₁^*,y₂^*,…y_m^*) .

За умов використання інших планівX≠X_opt, Y≠Y_opt на підставі основної нерівності теорії двоїстості можна стверджувати, що прибутки від реалізації продукції завжди менші, ніж витрати на її виробництво.

34.Друга та третя теореми двоїстості, їх економічна інтерпретація. Навести відповідні формули

Друга теорема двоїстості про доповнюючу нежорсткість.

Для того, щоб плани X^* та Y^* відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:

x_j^*(∑a_ijy_i^*-c_j)=0 (j=1,n; i=1,m)

y_i^*(∑a_ijx_i^*-b_i)=0 (i=1,m; j=1,n)

Наслідок: Якщо в результаті підстановки оптимального плану прямої задачі в систему обмежень цієї задачі і-те обмеження виконується як строга нерівність, то відповідний і-й компонент оптимального плану двоїстої задачі дорівнює нулю.

Якщо і-й компонент оптимального плану двоїстої задачі додат­ний, то відповідне і-те обмеження прямої задачі виконується для оптимального плану як рівняння.

Економічний зміст стосовно оптимального плану Х^* прямої задачі. Якщо для виготовлення всієї продукції в обсязі, що визначається оптимальним планом Х^*, витрати одного і-го ресурсу строго менші, ніж його загальний обсяг b_i, то відповідна оцінка такого ресурсу у*=0 (компонента оптимального плану двоїстої задачі), тобто такий ресурс за даних умов для виробництва не є «цінним».

Якщо ж витрати ресурсу дорівнюють його наявному обсягов b_i, тобто його використано повністю, то він є «цінним» для виробництва, і його оцінка y_i*>0.

щодо оптимального плану Y^* двоїстої задачі: у разі, коли деяке j-те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці j-го виду продукції перевищують її ціну с_j, виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої продукції x_j*=0.

Якщо витрати на виробництво j-го виду продукції дорівнюють ціні одиниці продукції c_j, то її необхідно виготовляти в обсязі, який визначає оптимальний план прямої задачі x_j*>0.

Третя теорема двоїстост. Компоненти оптимального плану двоїстої задачі у* (i=1,m) дорівнюють значенням частинних похідних від цільової функції F(b₁,b₂…b_m) за відповідними аргументами b_i, (i=1,m), або ðF/ðb_i=y_i^* i=1,2..m

Економічний зміст. Якщо взяти як приклад виробничу задачу, є питання: як змінюватиметься значення ЦФ (може вимірюватися в грошових одиницях) за зміни обсягів різних ресурсів (в тоннах, м², люд./год, га тощо).

Використовуючи третю теорему двоїстості, можна легко визначити вплив на зміну значення ЦФ збільшення чи зменшення обсягів окремих ресурсів: числові значення двоїстих оцінок показують, на яку величину змінюється ЦФ за зміни обсягу відповідного даній оцінці ресурсу y_i^*=∆F/∆b_i.

Отже, за умови незначних змін b_i замість ЗЛП у канонічній формі маємо нову задачу, де b_i замінено на b’_i= b_i+/∆b_i. Позначимо через X’ оптимальний план нової задачі. Для визначення F(X’) не потрібно розв’язувати нову задачу лінійного програмування, а достатньо скористатися формулою F(X’) –F(X*)= y_i^*∆b_i, де X* — оптимальний план задачі.

Економічний зміст третьої теореми двоїстості: відповідна додатна оцінка показує зростання значення ЦФ прямої задачі, якщо запас відповідного дефіцитного ресурсу збільшується на одну одиницю.