21. Економічна постановка та математична модель задачі лінійного програмування. Основні поняття задачі лінійного програмування

Лінійне програмування - математична дисципліна, присвячена теорії та методам розв'язання задач про екстремуми лінійних функцій на множинах n_мірного векторного простору, що задаються системами лінійних рівнянь і нерівностей. Лінійне програмування є окремим випадком математичного програмування. Одночасно воно - основа декількох методів вирішення завдань цілочисельного і нелінійного програмування. проходить послідовно наступні основні етапи:1. Постановка завдання. 2. Побудова (складання) математичної моделі. 3. Вибір методу рішення і рішення задачі. 4. Перевірка отриманого рішення на його адекватність досліджуваного явища і коректування моделі у разі потреби. 5. Реалізація знайденого рішення на практиці. Математична модель є абстрактним відображенням реального процесу (явища) і в міру своєї абстрактності може його характеризувати більш-менш точно. У побудові математичної моделі можна виділити наступні моменти: 1. Вибір невідомих величин Х = (х1, ..., хn), впливаючи на які можна змінювати поведінку досліджуваного процесу. Їх називають змінними, керованими параметрами, планом, стратегією. 2. Необхідно виділити мету (максимізація прибутку, мінімізація витрат та інше) функціонування досліджуваного процесу і записати її у вигляді математичної функції від обраних змінних. Така функція називається цільовою (функція мети, критерій оптимальності, критерій якості, показник ефективності) і дозволяє, змінюючи значення керованих параметрів x1, ..., xn, вибрати найкращий варіант з безлічі можливих. Будемо позначати функцію мети Z = f (X). 3. Запис у вигляді математичних співвідношень (рівнянь, нерівностей) умов, що накладаються на змінні. Ці співвідношення називають обмеженнями, вони можуть витікати, наприклад, через обмеженість ресурсів. Сукупність усіх обмежень складає область допустимих рішень (ОДР). Будемо позначати її буквою D (XD) .

Задача визначення оптимального плану виробництва: для деякої виробничої системи (цеху, підприємства, галузі) необхідно визначити план випуску n видів продукції Х = (х₁, х₂, …, х_n) за умови найкращого способу використанняїї наявних ресурсів. У процесі виробництва задіяні m ресурсів: сировина, трудові ресурси, технічне оснащення тощо. 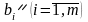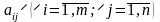Відомі загальні запаси ресурсів , норми витрат і-го ресурсу на виробництво одиниці j-ої продукції та прибуток з одиниці j-ої реалізованої продукції .

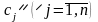Критерій оптимальності: максимум прибутку.

Позначимо через х₁, х₂, …, х_n обсяги виробництва відповідно першого, другого і т. д. видів продукції.

Оскільки на одиницю продукції 1-го виду витрачається 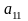ресурсу першого виду, то на виробництво першого виду продукції обсягом х₁ необхідно витратити а₁₁х₁ цього ресурсу. На другий вид продукції обсягом х₂ витрати першого ресурсу дорівнюватимуть а₁₂х₂ і т. д. На виробництво всіх видів продукції буде використано такий обсяг першого ресурсу: а₁₁х₁ + а₁₂х₂ + … + + а_1nx_n. Ця величина має не перевищувати наявного обсягу першого ресурсу — b₁. Отже, обмеження щодо використання першого ресурсу матиме вигляд: а₁₁х₁ + а₁₂х₂ + … + а_1nx_n ≤ b₁. Аналогічно записують обмеження стосовно використання всіх інших виробничих ресурсів. Прибуток від реалізації виготовленої продукції всіх видів становитиме: с₁х₁ + с₂х₂ + … + с_nx_n.

Загалом лінійна економіко-математична модель даної задачі матиме вигляд: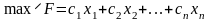

за умов: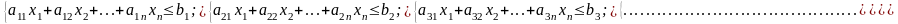

.

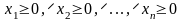Математична модель виробничої задачі може бути застосована для різних економічних задач, де виникає проблема вибору найкращого варіанта розподілу обмеженої кількості ресурсів, хоча з першого погляду може здаватися, що постановка задачі не стосується виробничих процесів. Наведемо кілька конкретних прикладів виробничих задач.