Вопрос 8: биномиальная схема испытаний. Формула Бернулли

Бином схема – послед-ть испыт-ий, удовл-ая 3 усл: 1.в кажд испыт - лишь 2 исхода: А={усп} и B={неусп} 2.исп-ия - независ, т.е. вер-ть «усп» в кажд испыт не завис от исхода в iм испыт, при k>i 3.вер-ть успеха в кажд испыт постоян P(A)=p P(неA)=1-p=q. Обозн Pn(k) – вер-ть того, что в исп-ях А появ-ся k раз. Pn(k)=Cknpkqn-k – фор-ла Бернулли, k=0,1,n. Док-во: (АА-k раз, ĀĀ- n-k раз; ĀĀ- n-k, АА-k раз)-Ckn. Р(ААĀĀ)=pkqn-k.

Замеч: 1.вер-ть появл усп А в n исп-ях хб 1 раз Pn(k≥1)=Pn(k=1)+Pn(k=2)+Pn(k=n)=1-p(=0)=1-qn . 2. вер-ть появл А в n исп-ях от k1 до k2 раз Pn(k1≤k≤k2)=Σ Pn(k).

Вопрос 9: Приближения формулы Бернулли: формула Пуассона

Если число испытаний велико, а вероятность p появления события в каждом испытании очень мала, то используют следующую формулу , где - число появлений события в n независимых испытаниях, = np (среднее число появлений события в n испытаниях), и говорят, что с.в.распределена по з-ну Пуассона. (Есть спец.таблицы для нахождения P (k), зная и . В виде таблицы это выглядит так

X	0	1	…	K	…
p			…		…

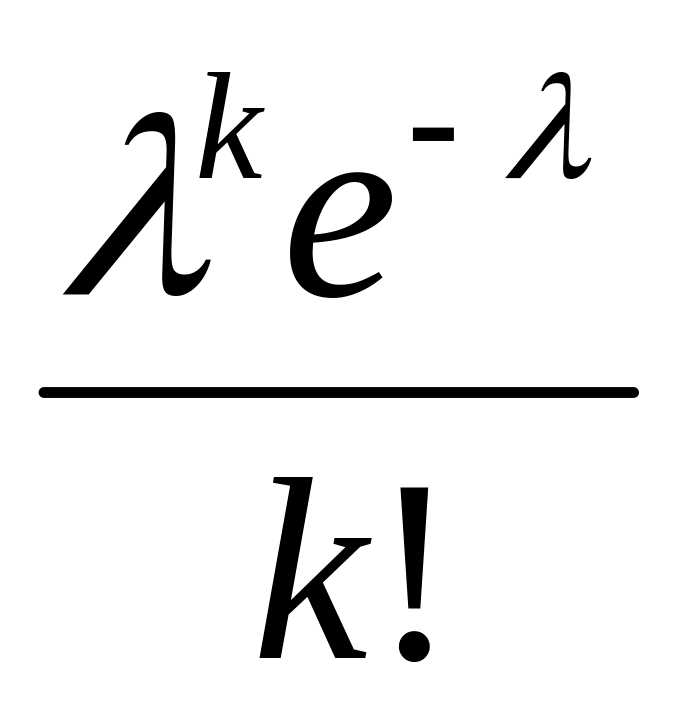
Какой смысл параметра  в пуассонском законе распределения?

 - это среднее число появлений события в n испытаниях, также можно отметить, что математическое ожидание и дисперсия дискретной с.в., распределенной по закону Пуассона, равны параметру  данного распределения.

Вопрос 10-11: приближения формулы Бернулли: локальная и интегральная теоремы Лапласа

Локал: если вер-ть р появл А в кажд испыт пост-но и 0<p<1, то вер-ть Pn(k) того, что А появ в n испыт-х равно k раз≈знач-ию ф-ии (тем точн, чем>n): Pn(k)=(1/√npq)*φ(x), где x=(k-np)/√npq. 1. при npq≥10 2. 1/n - порядок абсол погрешн-ти.

Интегр: если вер-ть р появл А в кажд испыт пост-но и 0<p<1, то вер-ть Pn(k1,k2) того, что А появ в n незав исп-ях от k1 до k2 раз при больш n≈Pn(k1,k2)=Ф(х2)-Ф(х1), где x2=(k2-np)/√npq, x1=(k1-np)/√npq. При npq≥10.

Вопрос 12: случайные величины. Типы случайных величин, способы их задания

Функ, задан на прос-ве элем-ных соб-й Ω- случ велич. Сл вел - кот в завис от исход опыта мож приним то или ин числен знач, неизв до опыта. +: случ вел- числов функ Х(), зад на прос-ве элем-ных соб-й  и измер относ-но поля соб-й S (измерим-ть: {:X()<x}S, для любо -<x<). Обозн они X, Y, X.

Типы сл вел: дискрет и непрерыв. Дискрет – если мн-во ее знач конечно или счетн. Непрер – приним-ая все знач из некот конечн ли бескон промеж.

Закон распр дискр сл вел: Х:х1,х2,..хn, P:p1,p2,..pn.Если рас {x=xi}, i=1..n соб-я несовм. P(x=x1)=p1 Pn=(x=xn)=pn. Закон распр- соответ-ие м ее возм-ми знач-ми и вер-ми их появл. Способ задан зак: таблич, графич и аналит. Табл: Х и Р. P(X<x1)=0. P(X<xn)=P(x=x1)+P(X=xn-1)=ΣPi. Граф: мн-уг-ик распр-ия. В прям-уг с-ме коорд нанос тчк с коор-ми (xi,pi), соседн тчк соед-ны прямым.По Y - Pi, по X - x. Пр: выпущ 100 билет. 1 б - 50 р, 10 бил – по 1р. выигрыша. Найти зак распр сл выигр для 1 бил. Реш: возм знач x: 0, 1, 50 (р) =>X:0|1|50; P:0,89|0,1|0,01.

Распред: равном, гипергеом, геметр, бином, Пуассона

Вопрос 13: гипергеометрическое распределение

Рассм схему без возвращ. Пусть им N об-тов, из них n-брак. N-n-станд. Взяли M детал, из них m брак. M-m-станд. N и M - параметры. Рассм x - кол-во брак детал среди M отобр-ых. Рассм соб, что х примет знач m: {X=m}, m=0,1..min {M,n}. PN,n,M(m)=(CmnCM-mN-n)/CMN.

Вопрос 14: геометрическое распределение

Рассм Р(А)=р, p-пар-тр. Исп-ия до 1 появл А, Х – кол-во испыт. Рассм соб, сост в том, что{Х=k}, k=1,2.. k=1 A, k=2 ĀA, P(x=k)=qk-1p, где k-1: Ā..ĀA.

Закон распр для него: Х: 1|2|3|k. Р: p|qp|q2p|qk-1p.

Геоме распред - бином схема и незав. испыт с 2-мя исход.

Вопрос 15: биномиальное распределение, параметры, числовые хар-ки

n незав испыт. Р(А)=р; n и р – парам-ры. X- число появл А ecg в n исп-ях. {x=k}, k=0,1..n. Pn(X=k)=Cknpkqn-k . Ckn -множ. возм-ть появл/не появ А. |x1=0, p1=qn; x2=1, p2=npqn-1; x3=2, P3=C2np2qn-2|.

E,D: xi={1-усп, 0-неусп}. xi={0,1}, p={q,p}. E(xi)=0q+1p=p, D(xi)=E(xi2)-E2(xi)=p-p2=p(1-p)=pq. X=x1+x2+xn=ni=1xi. E(X)=E(xi)=E(xi)=np. D(X)=D(xi)=D(xi)=npq.

Вопрос 16: распределение Пуассона

При усл: n→∞; p0, np= (const) - бином вер-ти: Pn(k)=(k/k!)e-. Осн пар-ры: n-вел, p-мал (<0,1), λ, np==const; X=кол-во успех в n испыт-ях (=0,1..). при n≥30, p≤0,1, np≤5.

Вопрос 17: арифметические операции над дискретными случайными величинами

2 случ вел - независ, если закон распр 1й из них не меняется от того, какие возм-ые знач приняла др сл вел. X: x1, x2, xn. Y:y1, y2, ym. P(X=xi, Y=yj)=Pij; i=1..n; j=1..m. Если X и Y незав, то вер-ть Pij=PiPj.

1.Произв-ем KX, сл вел Х на пост. вел. K - сл вел, кот приним знач kxi, i=1..n с вер-ми Pi.

2.k степ-ью сл вел x - сл вел, кот прин знач xki с вер-ью Рi.

3.Сумм (разн-ью, произв-ем) сл вел Х и У- сл вел Z, кот приним все возмож знач. Zij=xi+yj Zij=xi-yj Zij=xiyj, с вер-ью Pij=P(X=xi;Y=yj) i=1..n, j=1..m.