Вопрос 1: основные понятия теории вероятностей и матем-ой статистики

Теория вер-ей – матем-ая наука, изуч закономерности в случайных явлениях. Объектом иссл-ия ТВ явл-ся опыты, исходы которых однозначно не опред-ся условиями опыта. Вероятностная модель хар-ся: а)возможностью многократного повторения одного и того же эксперимента в одних и тех же условиях; б)большое число случайных факторов, кот влияют на исход эксперимента, не позволяет сделать опред-ые заключения об исходе эксперимента; в) чем больше проводим однотипных экспериментов, тем ближе относ-ая частота появления события к некоторой постоянной величине, кот наз-ся вероятностью события. Эксперимент – действия, осущ-ые при опред-ом комплексе условий (карты, монеты, кости). Возможный рез-т проведённого эксперимента наз-ся событием.

МС – наука и иск-во сбора и анализ дан. Задачи: оценка парам-ов, проверка стат гипот. Ген сов-ть –сов-ть всех мысл-ых наблюд, кот могли бы быть произв при данном реал комплексе усл. Выборка – часть объектов генсов-ти, выбр для анализа дан. Выб-ка объема n – знач призн-ка Х, измер на n объектах. В основе МС – выбор-й метод: выводы, получ по выбдан распр на всю генсов-ть.Случ выб-ка –послед-ть X1,.., Xn незав-ых один-во распр-ых сл вел-ин, распр-ие кажд их кот совпад с распр-ем ген сл вел. Распр-ие сл выб-ки: FX1, ..,Xn (x1,..,xn)=P{X1<x1,..,Xn<xn}=П(n|i=1) P{Xi<xi}=П(n|i=1) FXi(xi). ВР – посл-ть набл, упоряд-ых по возраст. Относ част Wi-отнош част встреч-ти признака к об-му выб-ки n. Накопл ч-та niн –сумма част предыд знач+текущ.

Вопрос 2: основные правила комбинаторики. Перестановки, размещения, сочетания

Комб-ка – теория конечных множ-тв (сов-ть элем-ов произв рода) конеч мн-ва-конеч число эл-ов. Осн прав – пр умнож: пусть треб-ся выполн k д-ий одно за др. Если 1е д-ие вып-ся n1 способами, 2е - n2, k - nk, то все k-д-ия вместе n=n1*n2*...*nk (одновр).

Факт-ал n! –произв-ие 1х n натур чис по ф-ле: n!=(n-1)!*n. (0!=1, 1!=1).

У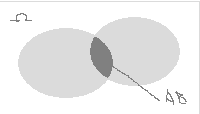 порядоч мн-во - если кажд эл-ту мн-ва пост-но в соотв-ие нек чис (№ эл-та с 1 до n). Перест-ки - разл упорядоч мн-ва, кот отлич-ся лишь порядк эл-ов. Pn=n!. 1,2,3: P3=3!=6. Перест с повтор: n эл-ов k типов- n=n1+n2+.+nk. Pn=(n,n2,nk)=n!/n!*n2!*nk!. (Ск перест в сл КАЗАК: n=5, k=3, 30).

Размещ из n-эл-ов по m-эл-ов - люб упоряд набор из мн-ва n-эл-ов. A из n по m=Cnm*m!=n!/(n-m)!. Важен поряд.

Сочет – произв-ое m-эл-ное подмн-во n-эл-го мн-ва. Число соч Cnm=n!/m!*(n-m)! Св-ва: Cn1=n; Cn0=1, Cnm=Cnn-m. Важно: кол-во эл-ов в m, 2 подм-ва д отлич 1им эл-ом, поряд следов эл в под-ах не важ. Cn2=n(n-1)/2.

Бином Ньют –целая полож степень сум 2х слаг-х (бинома), предс-я в виде сум ст-ей слаг-х - (a+b)n=an+Cn1an-1b+Cn2an-2b2+.+Cnman-mbm+bn=Σnm=0Cnman-mbm.

Вопрос 3: классификация событий. Пространство элементарных событий. Действия над событиями. Диаграммы Венна

Случайное событие – событие, которое в результате эксперимента может или произойти или нет. Достоверное событие – которое обязательно произойдет. Ω. Пример: выпадение на монете или герба или решки. Невозможное событие – которое заведомо никогда не произойдет. Θ.

Несколько событий образуют полную группу событий, если в результате проведения эксперимента хотя бы одно произойдет. Несовместными называются события А и В в случае, если появлении одного из них исключает появление другого. В противном случае они будут совместимыми. Равновозможные события – если в результате эксперимента ни одно из событий не является более возможным. Противоположные события – это два несовместимых события, из которых одно обязательно должно произойти.

И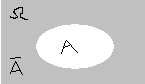 сход – элементарное (неразложимое) событие. Пространством элементарных событий (Ω) называется совокупность всех взаимоисключаемых простейших исходов эксперимента. Ω={w1,w2,...,wn} Множество исходов опыта образуют Ω, если: в результате опыта один из исходов обязательно произойдет (полнота); появление одного из исходов исключает появление остальных (несовместимость).

Диаграммы Вена. Суммой двух событий А и В называется А+В, состоящее из всех исходов, принадлежащих по крайней мере одному из событий А и В. Произведением двух событий А и В называется А*В, состоящее из исходов, принадлежащих и событию А, и событию В. Разностью двух событий А и В называется А-В, состоящее из исходов события А, не принадлежащих В. Свойства: А+В=В+А; АВ=ВА; (А+В)С=АС+ВС (дистрибутив-ть); //A=A; A+/A= Ω; A*/A=пустое мн-во; /A= Ω-A; A+ Ω= Ω; A* Ω=A; A+пустое мн-во=A; A*пустое мн-во=пустое мн-во.

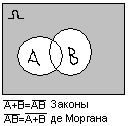+ Законы де Моргана.

А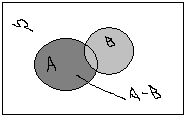 незав от В, если его условн вер-ть=безусл P(A/B)=P(A), и умнож незав соб: P(AB)=P(A)*P(B). Незав-ть соб взаимна, т.е. если А не завис от В, то и В не зав от А. Полн соб («подкова») –соб, кот вкл в себя все n эл-ные соб, и P(«подк»)=n/n=1.