Вопрос 15. Математические операции над случайными величинами.

Две случайных величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая случайная величина.

P(X=x_i, Y=y_j)=P_ij; i=1...n; j=1...n.

Если случайные величины X и Y независимы, то вероятность P_ij=P_i*P_j.

Произведением KX, случ. велич. Х на постоян. велич. k назыв. случайная величина, которая принимает значения kx_i, i=1...n с вероятностями P_i

k степенью случ. велич. x, x^k, k=1...n называется случайная величина, которая принимает значения x^k_i с вероятностью Р_i.

Суммой (разностью, произведением) случайной величины Х и У наз. случ. велич. Z. Z=X+Y Z=X-Y Z=XY. Которая принимает все возможные значения. Z_ij=x_i+y_j Z_ij=x_i-y_j Z_ij=x_i*y_j, с вероятностью P_ij=P(X=x_i;Y=y_j) i=1...n, j=1...n.

Вопрос 16: математическое ожидание случайной величины. Свойства мо

МО – сумма произведений всех возможных значений сл вел на их вероятности: Е(X)=ni=1xipi (при n). Св-ва:

1. мо постоянной =самой постоянной: Е(C)=C

2. постоянный множитель- за знак мо: Е(KX)=KE(X).Е(кX)=ni=1kxipi=kni=1xipi=KE(X).

3. мо суммы сл вел =сумме их мо: Е(X±Y)=Е(X)±Е(Y)

4. мо произведения независимых сл вел =произведению их мо: Е(XY)=Е(X)Е(Y)

5.если все значения сл вел Х изменяются на постояную величину С, на неё изменяется её мо: E(X+C)=E(X)+C. (E(X+C)=E(X)+Е(C)=E(X)+C, чтд).

6.мо отклонения сл вел отт св мо=0: Е(Х-Е(Х))=0. (Е(Х-Е(Х))=Е(Х)-Е(Х)=0, чтд).

7. мо альтерн сл вел (описыв рез-ат единич исп-ия в сх Бернул)=вер-ти полож-го исхода: Е(X)=p

8. мо бином сл вел=произв числа исп-ий на вер-ть полож-го исхода: Е(X)=np

9. мо пуасс сл вел: =np (пуасс – предел-ой по отн к бином): Е(X)=

10. мо геом сл вел (число исп-ий по сх Берн до 1го пол исх) ↑↓ вер-ти пол исх: Е(X)=1/p.

Вопрос 17: дисперсия случайной величины. Свойства дисперсии

Дисп D(X)– мо квадрата отклон сл вел от своего мо: D(X)=Е(X-Е(X))2. D(X)=ni=1(xi-E(xi))2pi. Ср квалратич отклон сигма σ =√D(X).

Св-ва:

1. дисп постоянной=0: D(C)=0. D(C)=E(C-E(C))2=E(C-C)2=E(0)2=0, чтд.

2.пост множ-ль - за знак D с возвед в ²: D(КX)2=К2D(X). D(KX)=E(KX-E(KX))2= E(K(X-E(X))2=K2X(X-E(X))2.

3.Дисп сл вел Х=разн-ти мо квадрата слвел Х и квадр её мо. D(X)=E(X2)-E2(X). D(X)=E(X-E(X))2=E(X2-2XE(X)+E2(X))=E(X2)-2E(X)E(X)+E2(X)=E(X2)-E2(X).

4.D суммы незав сл вел=сумме Dй: D(X±Y)=DX+DY.

D(X-Y)=E((X-Y)-E(X-Y))2=E((X-E(X))-(Y-E(Y)2=E((X-E(X))2-2(X-E(X))(Y-E(Y))+(Y-E(Y)2=D(X)-2E(X-E(X))E(Y-E(Y))+D(Y). 5.D(XY)=ЕX2ЕY2-(ЕX)2(ЕY)2. +DX=pq (альтер); DX=npq (бином); DX= (пуас); DX=q/p2 (геом).

Вопрос 19. Функция плотности распределения вероятностей одномерной случайной величины, свойства функции плотности. Геометрическая интерпретация.

P (x≤X-x+Δx)=F(x+Δx)-X(x)

(F(x+Δx)-F(x))/ Δx – плотность. lim_Δx->0(F(x+ Δx)-F(x))/Δx=F’(x).

Определение: функция плотности распределения ƒ(x)=F’(x)

Свойства ƒ(x): 1) ƒ(x)≥0; 2) P(a≤x<b)=F(b)-F(a)=|_a^bf(x)dx;

3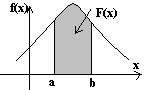 )F(x)=P(x<x)= |_-ω^bf(t)dt;

4)|_-ω^ωf(t)dt=F(x) |_-ω^ω= lim_x->+ωF(x)- lim_x->-ωF(x)=1.

Вопрос 20. Числовые характеристики непрерывных случайных величин.

Математическое ожидание Н.С.В. и его свойства.

Мат. ожидание Н.С.В. Х, возможные значения которой принадлежат всей оси ОХ, определяется равенством: М(Х)=интеграл от –бесконечности до бесконечности хf(x)dx, где f(x) - плотность распределения С.В. Х. Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу (а,b), то М(Х)=интеграл от ∫а b xf(x)dx. Все свойства мат. ожидания, указаны выше, для Д.С.В. Они сохраняются и для Н.С.В. 1) Мат. ожидание постоянной величины равно самой постоянной: М(С)=С.

2) Постоянный множитель можно выносить за знак мат. ожидания: М (СХ)=СМ (Х).

3) Мат. ожидание произведения взаимно независимых С.В. равно произведению мат. ожиданий сомножителей: М (Х1,Х2…Хn)=M(X1)*M(X2)…M(Xn).

4) Мат. ожидание суммы С.В. равно сумме мат. ожиданий слагаемых: М (Х1+Х2+Х3+…+Хn)=M(X1)+M(X2)+M(X3)+…+M(Xn).

Дисперсия Н.С.В. и ее свойства.

Дисперсия Н.С.В. Х, возможные значения которой принадлежат всей оси ОХ, определяется равенством: D(X)=интеграл от –бесконечности до бесконечности [x-M(X)]*2f(x)dx, или равносильным равенством: D(X)=интеграл от –бесконечности до бесконечности x*2f(x)dx – [M(X)]*2. В частности, если все возможные значения х принадлежат интервалу (a,b),то D(X)=интервал от а до b [x – M(X)]*2f(x)dx,или D(X)=интеграл от a до b x*2f(x)dx – [M(X)]*2. Все свойства дисперсии Д.С.В. сохраняются и для Н.С.В. 1) Д. постоянной равна нулю: D(C)=0.

2) Постоянный множитель можно выносить за знак Д., предварительно возведя его в квадрат: D (CX)=C*2D(X).

3) Д. суммы независимых С.В. равна сумме Д. слагаемых: D (X1+X2+…+Xn) =D(X1)+D(X2)+…+D(Xn).