Вопрос 1: основные понятия теории вероятностей.

Теория вероятностей – математическая наука, изучает закономерности в случайных явлениях. Объектом исследования ТВ являются опыты, исходы которых однозначно не определяется условиями опыта. Вероятностная модель характеризуются: а) возможностью многократного повторения одного и того же эксперимента в одних и тех же условиях; б)большое число случайных факторов, кот влияют на исход эксперимента, не позволяет сделать определенные заключения об исходе эксперимента; в) чем больше проводим однотипных экспериментов, тем ближе относительная частота появления события к некоторой постоянной величине, кот называется вероятностью события. Эксперимент – действия, осуществляемые при определенном комплексе условий (карты, монеты, кости). Возможный рез-т проведённого эксперимента называется событием.

Вопрос 2. Основное правило комбинаторики. Перестановки, размещения, сочетания. Бином Ньютона.

Комбинаторика – теория конечных множеств. Основное правило – правило умножения: пусть требуется выполнить k действий одно за другим. Если первое действие выполняется n₁ способами, второе - n₂, k – n_k, то все k-действия вместе выполняются n=n₁*n₂*...*n_k.

Различные упорядоченные множества, которые отличаются лишь порядками элементов, наз. Перестановками этого множества. P_n=n!

Размещением из n-элементов по m-элементов называется любой упорядоченный набор, выбранный из множества n-элементов. A из n по m =C из n по m *m! = n!/(n-m)!

Сочетание – произвольное m-элементное подмножество n-элементного множества.

C из n по m=n!/m!*(n-m)! Свойства: C из n по 1=n; C из n по 0=1.

Биномом Ньютона называют выражение (a+b)ⁿ=aⁿ+C_n¹*a^n-1*b+C_n²*a^n-2*b²+...+C_n^m*a^n-m*b^m+bⁿ=Σⁿ_m=0*C_n^m*a^n-m*b^m.

Вопрос 3. Классификация событий. Пространство элементарных событий. Действия над событиями. Диаграммы Вена.

Случайное событие – событие, которое в результате эксперимента может или произойти или нет. Достоверное событие – которое обязательно произойдет. Ω. Пример: выпадение на монете или герба или решки. Невозможное событие – которое заведомо никогда не произойдет. Θ.

Несколько событий образуют полную группу событий, если в результате проведения эксперимента хотя бы одно произойдет. Несовместными называются события А и В в случае, если появлении одного из них исключает появление другого. В противном случае они будут совместимыми. Равновозможные события – если в результате эксперимента ни одно из событий не является более возможным. Противоположные события – это два несовместимых события, из которых одно обязательно должно произойти.

И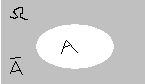 сход – элементарное (неразложимое) событие. Пространством элементарных событий (Ω) называется совокупность всех взаимоисключаемых простейших исходов эксперимента. Ω={w₁,w₂,...,w_n} Множество исходов опыта образуют Ω, если: в результате опыта один из исходов обязательно произойдет (полнота); появление одного из исходов исключает появление остальных (несовместимость).

Д 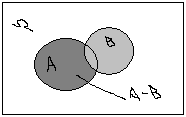иаграммы Вена. Суммой двух событий А и В называется А+В, состоящее из всех исходов, принадлежащих по крайней мере одному из событий А и В. Произведением двух событий А и В называется А*В, состоящее из исходов, принадлежащих и событию А, и событию В. Разностью двух событий А и В называется А-В, состоящее из исходов события А, не принадлежащих В. Свойства: А+В=В+А; АВ=ВА; (А+В)С=АС+ВС.