Вопрос№1. Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Взаимодействие зарядов. Закон Кулона.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия. Электрический заряд обычно обозначается буквами q или Q. Существует два рода электрических зарядов, условно названных положительными и отрицательными. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд. Одноименные заряды отталкиваются, разноименные – притягиваются. Электрический заряд дискре­тен, т. е. заряд любого тела составляет целое кратное от элементарного электриче­ского заряда е. ( ). Элек­трон ( ) и протон ( ) являются соответственно носителями элементарных отрицательного и положительного зарядов. Закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы. q₁ + q₂ + q₃ + ... +q_n = const. Единица электрического заряда – кулон (Кл) – электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. В истории развития физики имела место борьба двух теорий: дальнодействия и близкодействия. В теории дальнодействия принимается, что электрические явления определяются мгновенным взаимодействием зарядов на любых расстояниях. Согласно теории близкодействия, все электрические явления определяются изменениями полей зарядов, причем эти изменения распространяются в пространстве от точки к точке с конечной скоростью. Применительно к электростатическим полям обе теории дают одинаковые результаты, хорошо согласующиеся с опытом. Переход же к явлениям, обусловленным движением электрических зарядов, приводит к несостоятельности теории дальнодействия, поэтому современной теорией взаимодействия заряженных частиц является теория близкодействия. Закон Кулона: сила электростатического взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам и обратно пропорциональна квадрату расстояния r между ними: В векторной форме закон Кулона имеет вид где k коэффициент пропорциональности, зависящий от выбора системы единиц. В СИ коэффициент пропорциональности равен Тогда закон Кулона запишется в оконча­тельном виде: Величина называется электрической постоянной; она относится к числу фундаментальных физических постоянных и равна где фарад - единица электрической емкости.

Вопрос№2. Напряженность электростатического поля. Принцип суперпозиции. Расчет напряженности поля тонкого заряженного тела.

Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила; значит, в пространстве, окружающем электрические заряды, существует силовое поле. В данном случае говорят об электрическом поле – поле, посредством которого взаимодействуют электрические заряды. Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в эту точку поля:

.

в вакууме .

Направление вектора совпадает с направлением силы, действующей на положительный заряд.

Единица напряженности электростатического поля – ньютон на кулон (Н/Кл) : 1 Н/Кл – напряженность такого поля, которое на точечный заряд 1 Кл действует с силой в 1 Н; 1 Н/Кл =1 В/м. Графически электростатическое поле изображают с помощью линий напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора .

Линиям напряженности приписывается направление, совпадающее с направлением вектора напряженности. Так как в каждой данной точке пространства вектор напряженности имеет лишь одно направление, то линии напряженности никогда не пересекаются.

Рассмотрим определение значения и направления вектора напряженности в каждой точке электростатического поля, создаваемого системой неподвижных зарядов

К кулоновским силам применим рассмотренный в механике принцип независимости действия сил, т.е. результирующая сила , действующая со стороны поля на пробный заряд , равна векторной сумме сил – приложенных к нему со стороны каждого из зарядов

и , где - напряженность результирующего поля, а напряженность поля, создаваемого зарядом . Получим

Формула выражает принцип суперпозиции электростатических полей, согласно которому напряженность результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Вопрос№3.Электрический диполь и его поле.

Электрический диполь - система двух равных по модулю разноименных точечных зарядов (+Q, -Q), расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля.

Вектор , направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя.

Вектор, совпадающий по направлению с плечом диполя и равный произведению заряда на плечо , называется электрическим моментом диполя или дипольным моментом.

Согласно принципу суперпозиции, напряженность поля диполя в произвольной точке

где и - напряженности полей, создаваемых соответственно положительным и отрицательным зарядами.

Вопрос№4. Силовые линии электрического поля. Поток вектора. Электрическая теорема Гаусса и ее применение для расчетов полей.

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились проводить их с определенной густотой. Число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора . Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль которой образует угол с вектором , равно , где – проекция вектора на нормаль к площадке dS .

Величина называется потоком вектора напряженности через площадку dS. Единица потока вектора напряженности электростатического поля 1 . Для произвольной замкнутой поверхности S поток вектора через эту поверхность , где интеграл берется по замкнутой поверхности S.

Поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре .

Этот результат справедлив для замкнутой поверхности любой формы.

Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора будет равен , т. е.

Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на .

Рассмотрим применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме:

1. Поле равномерно заряженной бесконечной плоскости.

Бесконечная плоскость заряжена с постоянной поверхностной плотностью ( – заряд приходящийся на единицу поверхности). Согласно теореме Гаусса , , откуда

2.Поле двух бесконечных параллельных разноименно заряженных плоскостей

Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями и . Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой , а вне объема, ограниченного плоскостями, равна нулю.

3.Поле равномерно заряженной сферической поверхности.

Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью . по теореме Гаусса откуда

( ).

При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. Если r' < R, тo замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е = 0).

4. Поле объемно заряженного шара.

Напряженность поля вне равномерно заряженного шара описывается формулой : ( ),

а внутри его изменяется линейно с расстоянием согласно выражению ( ).

Вопрос№5.Работа электрического поля. Теорема о циркуляции напряженности электрического поля. Потенциал. Эквипотенциальная поверхность. Связь потенциала с напряженностью.

Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд , то сила, приложенная к заряду, совершает работу.

Работа силы на элементарном перемещении dl равна

.

Так как , то .

Работа при перемещении заряда из точки 1 в точку 2

не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек.

Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т. е.

.

Силовое поле, обладающее свойством

,

называется потенциальным. Интеграл, стоящий в левой части соотношения наз. циркуляцией вектора Е вдоль замкнутого контура L. Итак, циркуляция вектора напряженности электростатического поля точечного заряда q вдоль произвольного замкнутого контура проведенного в поле, равна нулю. Условие является необходимым и достаточным для того, чтобы поле напряженностью Е было потенциальным.

Формула

справедлива только для электростатического поля.

Потенциал электростатического поля и его связь с напряженностью

Потенциал в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.

Потенциал поля, создаваемого точечным зарядом Q, равен

.

Работа, совершаемая силами электростатического поля при перемещении заряда из точки 1 в точку 2, может быть представлена как

,

Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2.

,

,

,

.

Потенциал – физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.

Единица потенциала – вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В=1 Дж/Кл).

Работа по перемещению единичного точечного положительного заряда из одной точки в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и , равна . Та же работа равна . Приравняв оба выражения, можем записать ,

где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осей у и z, можем найти вектор : ,

где , , – единичные векторы координатных осей х, у, z.

Из определения градиента следует, что , или

т. е. напряженность поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности поля направлен в сторону убывания потенциала.

Эквипотенциальными поверхностями называются– поверхности, во всех точках которых потенциал имеет одно и то же значение.

Если поле создается точечным зарядом, то его потенциал

.

Вектор всегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора ортогональны этим поверхностям.

Вопрос№6. Проводник в электрическом поле. Распределение заряда в проводнике. Электростатическое поле в полости.

Все тела состоят из атомов. Проводниками наз. в-ва, в к-ых есть свободные электрические заряды, способные перемещаться под действием электрического поля на макроскопическом расстоянии.

Если поместить проводник во внешнее электростатическое поле, то на заряды, находящиеся в проводнике, проводника будет действо­вать электростатическое поле, в результа­те чего заряды начнут перемещаться. Переме­щение зарядов (ток) продолжается до тех пор, пока не установится равновесное рас­пределение зарядов, при котором электро­статическое поле внутри проводника обра­щается в нуль.

На одном конце проводника будет скапливаться избыток положитель­ного заряда, на другом – избыток отрица­тельного. Эти заряды называются индуци­рованными. Индуцированные заряды исчезают, как только проводник удаляется из электрического поля.

Индуци­рованные заряды распределяются на внешней поверхности проводника. Явле­ние перераспределения поверхностных за­рядов на проводнике во внешнем электро­статическом поле называется электроста­тической индукцией.

Отсутствие поля внутри проводника означает, что потенциал во всех точках внутри проводника постоя­нен ( ), т. е. поверхность провод­ника в электростатическом поле является эквипотенциальной.

Если проводнику сообщить некоторый заряд Q, то нескомпенсированные заряды располагаются только на поверхности про­водника. Это следует из теоремы Гаусса:

так как во всех точках внутри поверхности D = 0.

(где – электрическое смещение или электрическая индукция ).

Вопрос№7. Поверхностная плотность заряда. Граничные условия на границе проводника с вакуума.

Поверхностная плотность заряда – заряд, приходящийся на единицу площади.

Найдем взаимосвязь между напряжен­ностью Е поля вблизи поверхности заря­женного проводника и поверхностной плотностью зарядов на его поверхности. Для этого применим теорему Гаусса к бес­конечно малому цилиндру с основаниями , пересекающему границу проводник - диэлектрик.

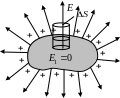
Согласно теореме Гаусса, поток вектора электрического смещения ( ) равен сумме зарядов ( ), охватываемых поверхно­стью: , т.е.

или

где – диэлектрическая проницаемость среды, окружающей проводник.

Таким образом, напряженность элек­тростатического поля у поверхности про­водника определяется поверхностной плотностью зарядов.

Граничные условия на границе проводника с вакуумом.

Рассмотрим заряженный проводник. Выберем на нем площадку dS такую малую, что значение вектора E в любой точке одинаково. Сигма=dq/dS=q/S/ Воспользуемся для нахождения вектора Е теоремой Гаусса Ф= E*dS=q/(эпсилант нулевое). Это и есть граничное условие.

Вопрос№8. Дифференциальная форма теоремы Гаусса. Уравнение Пуассона. Общая задача электростатики.

Объёмная плотность заряда определяется по аналогии с плотностью массы как отношение заряда dq к физически бесконечно малому объёму dV, в котором заключён этот заряд: .Зная плотность заряда в каждой точке пространства , можно найти суммарный заряд: . Данной формуле можно придать вид .Заменив поверхностный интеграл объёмным, получим .Соотношение , к которому мы пришли, должно выполняться для любого произвольно выбранного объёма V. Это возможно лишь в том случае , если значение подынтегральных функций в каждой точке пространства одинаковы. Следовательно дивергенция вектора E связана с плотностью заряда в той же точке равенством . Это равенство выражает теорему Гаусса в дифференциальной форме.

Уравнение Пуассона: Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает: электростатическое поле, стационарное поле температуры, поле давления, поле потенциала скорости в гидродинамике. Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: Δφ = f,где Δ — оператор Лапласа или лапласиан, а f — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

В декартовой системе координат оператор Лапласа записывается в форме и уравнение Пуассона принимает вид: .Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):Δφ = 0.

Общая задача электростатики: Уравнение Пуассона является одним из краеугольных камней электростатики. Нахождение φ для данного f — важная практическая задача, поскольку это обычный путь для нахождения электростатического потенциала для данного распределения заряда. В единицах системы СИ:

, где — электростатический потенциал (в вольтах), — объёмная плотность заряда (в кулонах на кубический метр), а — диэлектрическая проницаемость вакуума (в фарадах на метр). В единицах системы СГС: . В области пространства, где нет непарной плотности заряда, имеем:

, и уравнение для потенциала превращается в уравнение Лапласа:

Вопрос№9. Емкость уединенного проводника. Конденсатор. Емкость конденсаторов различной конфигурации. Соединение конденсаторов.

Рассмотрим уединенный проводник, т. е. проводник, который удален от других проводников, тел и зарядов. Его потенци­ал прямо пропорциона­лен заряду проводника.

Из опыта следует, что разные проводники, будучи одинаково заряженными, принимают различные по­тенциалы. Поэтому для про­водника можно записать:

.

Величину называют электроемкостью (или просто емкостью) уединенного проводника.

Единица электроемкости - фарад (Ф).

1 Ф — емкость такого уединенного проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1 Кл.

Конденсатор – устройство, обладающие способностью при малых раз­мерах и небольших относительно окружа­ющих тел потенциалах накапливать зна­чительные по величине заряды, иными сло­вами, обладать большой емкостью.

Конденсатор состоит из двух провод­ников (обкладок), разделенных диэлект­риком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэ­тому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коакси­альных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на: