Министерство высшего и профессионального образования Российской Федерации

Уральский государственный технический университет - УПИ

Теория поля

Задания для самостоятельной работы

по курсу " Высшая математика" для

студентов всех форм обучения всех

специальностей

Екатеринбург, 2002

УДК 517

Составители Д.Х.Даянов, Е.М.Пампура, М.А.Вигура, И.П.Ишунькина, Н.В.Колмогорова, Н.Г.Рыжкова

Научный редактор проф.,докт.физ.-мат. наук А.Б.Соболев

Теория поля: Задания для самостоятельной работы по курсу " Высшая математика" / Д.Х.Даянов, Е.М.Пампура, М.А.Вигура, И. П.Ишунькина, Н.В. Колмогорова, Н.Г.Рыжкова

Екатеринбург: УГТУ - УПИ, 2002. с.

Работа содержит ответы к домашним и контрольным заданиям по программному разделу курса. Содержит 12 задач в 31 вариантах.

Подготовлено кафедрой " Высшая математика".

 Уральский государственный

технический университет -УПИ, 2002

Вариант 1

Задача 1.1. Найти производную скалярного поля u(x,y,z) в точке М по направлению проходящей через эту точку нормали к поверхности S,образующей острый угол с положительным направлением оси Oz.

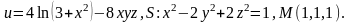
Задача 2.1. Найти угол между градиентами скалярных полей u(x,y,z) и v(x,y,z) в точке М,где

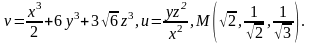
Задача 3.1. Найти векторные линии в векторном поле ,

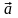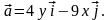
Задача 4.1. Найти поток векторного поля через часть поверхности S, вырезаемую плоск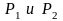остями (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями),

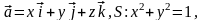
Задача 5.1. Найти поток векторного поля через часть плоскости Р, расположенную в первом октанте (нормаль образует острый угол с осью Oz),

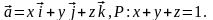
Задача 6.1. Найти поток векторного поля через часть плоскости P, расположенную в первом октанте (нормаль образует острый угол с осью Oz,

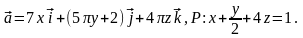
Задача 7.1. Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).

Задача 8.1. Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).

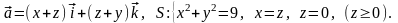
Задача 9.1. Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).

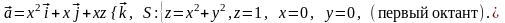
Задача 10.1. Найти работу силы F при перемещении вдоль линии L от точки М к точке N.

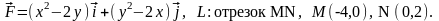
Задача 11.1. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t).

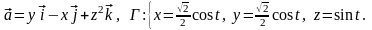
Задача 12.1. Найти модуль циркуляции векторного поля вдоль контура Г .

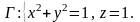
Вариант 2

Задача 1.2. Найти производную скалярного поля u(x,y,z) в точке М по направлению проходящей через эту точку нормали к поверхности S,образующей острый угол с положительным направлением оси Oz.

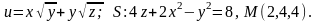
Задача 2.2. Найти угол между градиентами скалярных полей u(x,y,z) и v(x,y,z) в точке М, где

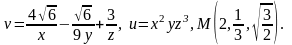
Задача 3.2. Найти векторные линии в векторном поле ,

Задача 4.2. Найти поток векторного поля через часть поверхности S, вырезаемую плоскостями (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями),

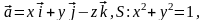
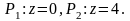
Задача 5.2. Найти поток векторного поля через часть плоскости Р, расположенную в первом октанте (нормаль образует острый угол с осью Oz),

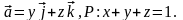
Задача 6.2. Найти поток векторного поля через часть плоскости P, расположенную в первом октанте (нормаль образует острый угол с осью Oz,

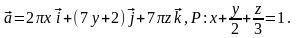
Задача 7.2. Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).

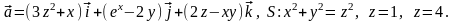
Задача 8.2. Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).

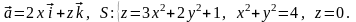
Задача 9.2. Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).

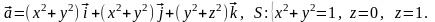
Задача 10.2. Найти работу силы F при перемещении вдоль линии L от точки М к точке N.

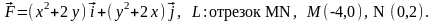
Задача 11.2. Найти циркуляцию векторного поля вдоль контура Г (в направлении, соответствующем возрастанию параметра t).

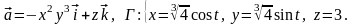
Задача 12.2. Найти модуль циркуляции векторного поля вдоль контура Г .