Приклади

1. Задані вектори (1; 2; 3), (-1; 0; 3), (2; 1; -1) і (3; 2; 2) в деякому базисі. Показати, що вектори , і утворюють базис і знайти координати вектора в цьому базисі.

Розв'язок. Вектори утворюють базис, якщо вони лінійно незалежні, тобто, якщо рівняння, що входять в систему:

лінійно незалежні.

Тоді .

Ця умова виконується, якщо визначник матриці системи відрізняється від нуля.

;

;

.

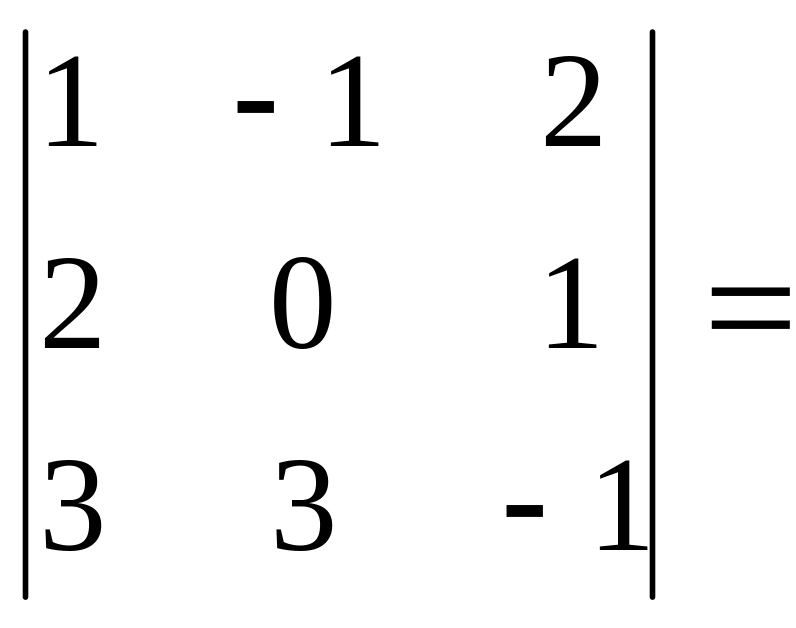
Для розв’язання цієї системи скористаємося методом Крамера.

₁ =

;

₂ =

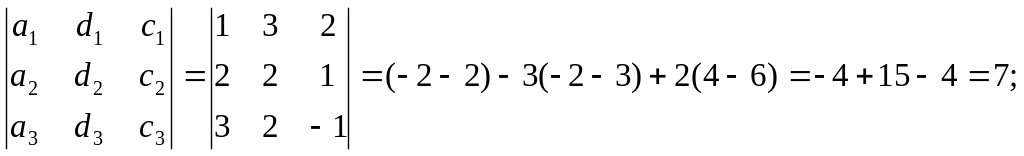
₃ =

Отже, координати вектора в базисі , , : { -1/4, 7/4, 5/2}.

2. Знайти (5 + 3 )(2 - ), якщо

Розв'язок.

10  - 5  + 6  - 3  = 10 , так як .

3. Знайти кут між векторами і , якщо

.

Тобто = (1, 2, 3), = (6, 4, -2)

 = 6 + 8 – 6 = 8:

.

cos =

4. Знайти скалярний добуток (3 - 2 )(5 - 6 ), якщо

Розв'язок. 15  - 18  - 10  + 12  =

15 + 1236 = 240 – 336 + 432 = 672 – 336 = 336.

5. Знайти кут між векторами і , якщо .

Розв'язок. Згідно умові, координати векторів: =(3, 4, 5), =(4, 5, -3).

Отже,  = 12 + 20 - 15 =17 :

.

cos =

5. Знайти скалярний добуток векторів і , якщо

Розв'язок.

( )( ) =

=

10 + 27 + 51 + 135 + 72 + 252 = 547.

6. Знайти векторний добуток векторів і .

Розв'язок.

Координати векторів: = (2, 5, 1); = (1, 2, -3). Отримаємо:

.

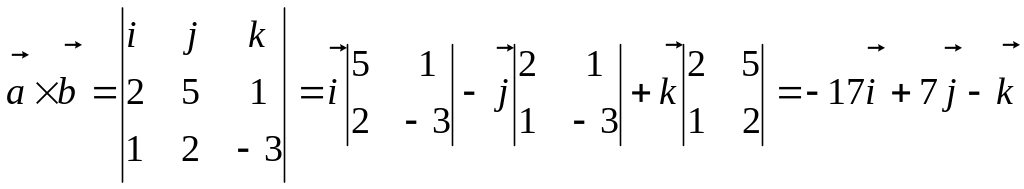7. Обчислити площу трикутника з вершинами А(2,2,2), В(4,0,3), С(0, 1, 0).

Розв'язок. Обчислимо координати векторів:

Векторний добуток цих векторів дорівнює:

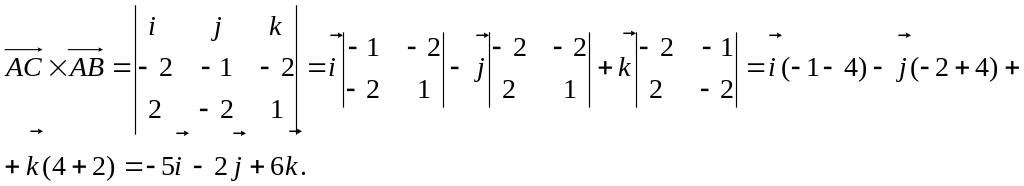Згідно властивості векторного добутку, маємо:

Площа трикутника дорівнює половині площі паралелограма, отже (ед²).

8. Обчислити суму векторів, їх скалярний добуток, а також проекцію вектора на вектор :

Розв'язок.

9. Довести, що точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежать в одній площині.

Розв'язок.

Знайдемо координати векторів:

Знайдемо мішаний добуток отриманих векторів:

,

Таким чином, отримані вище вектори компланарні, отже точки A, B, C і D лежать в одній площині.

10. Знайти рівняння прямої, яка проходить через точку А(1, 2) перпендикулярно вектору (3, -1).

Розв'язок. Складемо при А = 3 і В = -1 рівняння прямої: 3х – у + С = 0. Для знаходження коефіцієнта С підставимо в отриманий вираз координати заданої точки А.

Отримаємо: 3 – 2 + C = 0, отже С = -1.

Шукане рівняння: 3х – у – 1 = 0.

11. Задано загальне рівняння прямої х – у + 1 = 0. Знайти рівняння цієї прямої у відрізках.

С = 1, , а = -1, b = 1.

12. Дано загальне рівняння прямої 12х–5у –65 = 0. Потрібно записати різні типи рівнянь цієї прямої.

Рівняння цієї прямої у відрізках: ,

Рівняння цієї прямої з кутовим коефіцієнтом: (ділимо на 5)

нормальне рівняння прямої:

; cos = 12/13; sin = -5/13; p = 5.

13. Пряма відтинає на координатних осях рівні додатні відрізки. Скласти рівняння прямої, якщо площа трикутника, утвореного цими відрізками дорівнює 8 см².

Розв'язок.

Рівняння прямої має вид: , a = b = 1; ab/2 = 8; a = 4; -4.

a = -4 не задовольняє умові задачі.

Отже: або х + у – 4 = 0.

14. Визначити кут між прямими: y = -3x + 7; y = 2x + 1.

Розв’язок. k₁ = -3; k₂ = 2 tg = ;  = /4.

15. Задані вершини трикутника А(0; 1), B(6; 5), C(12; -1). Знайти рівняння висоти, яка проведена з вершини С.

Розв'язок. Знаходимо рівняння сторони АВ:

; 4x = 6y – 6;

2x – 3y + 3 = 0;

Шукане рівняння висоти має вид: Ax + By + C = 0 або y = kx + b.

k= . Тоді y= . Так як висота проходить через точку С, то її координати задовольняють даному рівнянню: звідки b=17. Отже: або 3x + 2y – 34 = 0.

16. Виходячи з рівняння прямої: -2x+8y+12=0, визначити відстань прямої від початку координат.

Розв'язок. 1,45.