23. Характеристики фнч Бесселя

Фильтр нижних частот Бесселя отличается от других фильтров тем, что имеет оптимальную фазочастотную характеристику с точки зрения неискаженной передачи сигнала в полосе пропускания. Проходящий через фильтр сигнал не изменит своей формы, если все гармоники сигнала будут задерживаться в фильтре на одно и то же время, т.е. ФЧХ фильтра будет иметь линейный характер. Фильтр Бесселя обеспечивает наилучшее приближение реальной ФЧХ к идеальной линейной зависимости, но имеет меньший наклон АЧХ в полосе подавления и переходной области, чем фильтры Баттерворта и Чебышева. Частота среза фильтра Бесселя определяется не по АЧХ, а по излому характеристики группового времени задержки τ(ω), пример которой изображен на рис. 5.9.

Рис. 5.9. Характеристика группового времени задержки ФНЧ Бесселя 4-го порядка

Передаточная функция фильтра Бесселя n-го порядка имеет вид: ,

где k – коэффициент усиления фильтра на постоянном токе; B_n(p) – полином Бесселя:

,

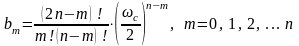где b_m – числовые коэффициенты полинома Бесселя; n – порядок фильтра, определяемый числом реактивных элементов; ω_c – частота среза ФНЧ Бесселя – предельная частота, на которой сохраняется постоянное время замедления, вносимое фильтром.

Частотная характеристика времени замедления фильтра Бесселя τ(ω) в диапазоне частот от 0 до ω_c монотонно спадает от значения на частоте ω = 0, равного τ(0) ≈ 1/ω_c, до значения на частоте ω = ω_с при увеличении порядка фильтра время замедления приближается к постоянному значению. При этом обеспечиваются условия неискаженной передачи сигнала сложной формы.

АЧХ фильтра Бесселя уступает характеристикам фильтров Баттерворта и Чебышева, т.к. имеет меньшую крутизну спада в переходной частотной области.

Для заданного времени замедления τ(0) в полосе пропускания можно приблизительно найти частоту среза ω_c ФНЧ и частоту по уровню затухания АЧХ 3 дБ (для n ≥ 3):

24. Инверсный фнч Чебышева

Инверсный и эллиптический ФНЧ Чебышева относятся к классу неполиномиальных фильтров, т.е. тех, которые описываются передаточной функцией общего вида:

при ненулевых коэффициентах не только знаменателя, но и числителя.

Инверсный фильтр Чебышева имеет АЧХ, которая монотонна в полосе пропускания и содержит пульсации в полосе задерживания. На рис. 5.11 показана ЛАЧХ инверсного фильтра Чебышева 4-го порядка.

Рис. 5.11 ЛАЧХ инверсного фильтра Чебышева 4-го порядка

АЧХ инверсного ФНЧ Чебышева описывается выражением: ,

где ε – постоянное число, С_n(x) – полином Чебышева первого рода степени n:

Величиной ε определяется неравномерность коэффициента передачи в полосе задерживания (ω ≥ ω₁):

.

Размах пульсаций составляет , или в логарифмическом масштабе для затухания:

Отсюда можно определить величину ε:

Частота среза ω_с для инверсного фильтра Чебышева любого порядка определяется по уровню затухания 3 дБ.

Для определения требуемого порядка n_тр инверсного ФНЧ Чебышева

С учетом ɛ получим: .

Анализ последнего выражения показывает,что требуемый порядок инверсного ФНЧ Чебышева примерно требуемому порядку ФНЧ Чебышева, имеющего допустимое затухание в полосе пропускания α₁ = 3 дБ.

Эллиптический фильтр Чебышева имеет АЧХ, содержащую пульсации как в полосе пропускания, так и в полосе задерживания. АЧХ эллиптического ФНЧ Чебышева имеет самый крутой наклон на частотах выше ω_с.