54. Геометрическая интерпретация средней производительности, понятие коэффициента эластичности.

Средняя производительность

(10.3)

отражает средний темп изменения показателя эффективности при увеличении фактора в диапазоне от нуля до заданного значения

Если под у понимать не показатель эффективности производ­ства, а производственные затраты на выпуск продукции, то рас­сматриваемое отношение следует интерпретировать как себе­стоимость единицы продукции.

Если — линейная функция, в которой величи-

на интерпретируется как постоянная составляющая затрат, а коэффициент регрессии а_х — как текущий расход на единицу продукции, то себестоимость единицы продукции, рассчитанная по формуле (10.3), будет убывать с ростом производства за счет уменьшения доли постоянных расходов по сравнению с пере­менной составляющей

Коэффициент эластичности

(10.4)

характеризует относительное изменение результата производства на единицу относительного изменения производственного фактора. Численно он равен отношению дополнительного про­дукта данного фактора (предельной производительности) к сред­ней производительности:

55. Понятие изокванты. Предельная норма заменяемости ресурсов.

Предельная норма заменяемости может рассчитываться, когда число факторов более единицы. Здесь необходимо ввести новое понятие — изокванты производственной функции. В общем слу­чае она определяется как поверхность в К-мерном пространстве производственных факторов на которой показатель эф-

фективности производства постоянен; таким образом, уравнение изокванты имеет вид

(10.5)

Если число факторов равно двум (или когда при К>2 анали­зируются только два фактора то геометрически изокванта может быть изображена как линия на плоскости . Задавая

различные значения константы в уравнении (10.5), можно полу­чить набор изоквант.

Рассмотрим ситуацию, когда все факторы, за исключением двух указанных, фиксированы. В этом случае дифференциал (приращение) определяется соотношением

На изокванте приращениепо определению,

должно быть равно нулю; следовательно,

(10.6)

Преобразовывая это равенство, получим dXi=H_x._Xj(x_h...,x_K)dXj,

где

Величина называется предельной нормой заме-

няемости фактора фактором Смысл этого названия раскры­вается следующей приближенной экономической интерпретаци­ей соотношения (10.6):

для сохранения заданного уровня производства в случае изменения фактора на единицу изменение фак-

тора должно быть равно предельной норме заменяемости

Из (10.6) следует, что для любой пары факторов норма заме­няемости фактора фактором связана с нормой заменяемости фактора X: фактором х, соотношением

(10.8)

20

Если связь обоих факторов с результатом такова, что их из­менение действует на у в одном направлении (например, рост как так и либо увеличивает, либо уменьшает у), иначе гово­ря, дополнительные продукты по обоим факторам имеют оди­наковый знак, норма заменяемости будет отрицательной. Это значит, что для сохранения постоянного уровня у уменьшение одного фактора должно компенсироваться ростом другого фак­тора и обратно — при увеличении одного фактора допустимо уменьшение другого. Это «естественное» поведение зависимос­тей при правильной организации производства, если оба факто-

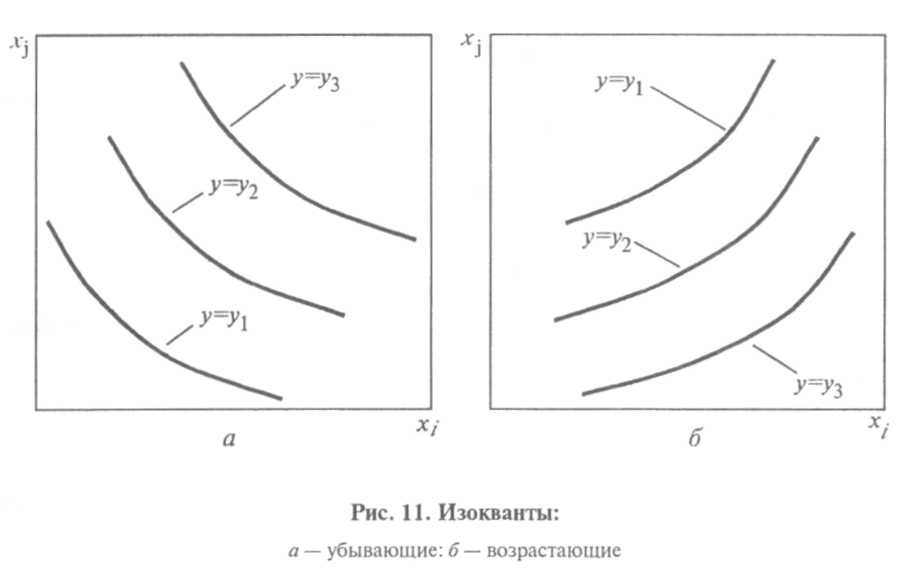
pa имеют характер ресурсов¹. В этой ситуации характер изоквант будет таким, как у изоквант, показанных на рисунке 11, а («убывающие» линии в плоскости

В противном случае (дополнительные продукты имеют разные знаки) предельная норма заменяемости положительна, и, следовательно, для сохранения заданного уровня у рост одного фактора должен сопровождаться ростом другого. Если оба фак­тора являются ресурсами, то положительная норма заменяемости может свидетельствовать либо о грубых нарушениях в организа­ции производства, либо об ошибках в построении производ­ственной функции, например вследствие неверной статистичес­кой обработки выборки при построении уравнения регрессии (на это утверждение также распространяется отмеченное выше ис­ключение). Если же один из факторов — ресурс, а другой количе­ственно характеризует некоторый негативный эффект, например эродированность пашни, то положительная норма заменяемости свидетельствует о «правильном характере» производственной функции. В этом случае увеличение негативного эффекта и дол­жно компенсироваться ростом затрачиваемых ресурсов. Харак­тер изоквант при этом будет таким, как у показанных на рисунке 11, б («возрастающие» линии в плоскости