52. Экономические характеристики производственных функций и их использование в землеустройстве и земельном кадастре.

Производственные функции как результат обобщения опыта, прямых наблюдений и экспериментов в землеустроительной практике служат концентрированным источником исходной ин­формации; можно выделить три основных класса задач, в кото­рых целесообразно их использовать:

задачи прогнозирования¹, в которых граничные условия либо во­обще не задаются в явном виде, либо играют чисто номинальную роль (определяют область допустимых значений аргументов фун­кции регрессии);

оптимизационные задачи, в которых эти условия играют актив­ную роль факторов, формирующих облик оптимального решения;

задачи экономического анализа состояния и использования зе­мель, изучения других процессов, существенных для землеуст­ройства.

На первый взгляд к самостоятельному классу относятся опти­мизационные задачи, в которых оптимальное решение находится в виде экстремума производственной функции внутри области допустимых значений аргументов однако в действительности в сложных задачах факт нахождения экстремума внутри области допустимых значений устанавливается после его отыска­ния, и, следовательно, такие задачи — частный случай задач вто­рого из названных классов.

В приводимых ниже определениях предполагается заданной функциональная зависимость результатов производства от ряда факторов причем эта функция имеет первые про-

изводные по всем аргументам. Рассматриваемые характеристики имеют по преимуществу экономический смысл, и соответствен­но основная область их применения — анализ влияния различ­ных факторов на эффективность производства. На микроэконо­мическом уровне в качестве анализируемого результата произ­водства могут выступать как обобщенные экономические показа­тели (валовой продукт, чистый доход и т. п.), так и частные (урожайность конкретной культуры, стоимость продукции расте­ниеводства и т. д.). Далее в данном разделе величина у, как пра­вило, называется показателем эффективности производства или просто показателем эффективности.

Дополнительный продукт фактора х (или иначе предельная про­изводительность) определяется частной производной:

(10.1)

причем все остальные факторы считаются постоянными.

По самому смыслу производной ~ она характеризует скорость (темп) изменения показателя эффективности «в данной точке» при изменении фактора и заданных значениях других произ­водственных факторов¹. Приближенно равна приросту Ау про­дукции за счет увеличения фактора на единицу

Если известен дополнительный продукт фактора, то при малых приращениях новое значение показателя эффективно­сти может быть оценено по формуле

(10.2)

Эта формула «предсказывает» линейное изменение показате­ля эффективности при изменении данного фактора, что в общем случае верно лишь при небольших значениях Исключение составляет случай линейной зависимости показателя эффектив­ности от фактора Например, если однофакторная производ­ственная функция линейна: то формула (10.2), с уче­том того что

справедлива при любых значениях В других случаях оценка

¹ По этой причине дополнительный продукт фактора относят к так называе­мым точечным оценкам.

изменения у по формуле (10.2) при больших значениях может приводить к неприемлемо большим погрешностям.

Если известно, что рассматриваемый показатель эффективно­сти у достигает максимума внутри области допустимых значений производственных факторов то максимальное значение

у и соответствующие ему оптимальные значения фактора могут быть определены путем решения системы уравнений:

А(х_ь...,х*Н ]

где зависимости предельных продуктов от производственных факторов определяются по формуле (10.1) при заданной зависи­мости

Средняя производительность

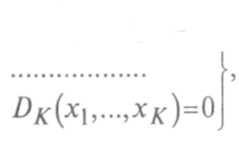
(10.3)

отражает средний темп изменения показателя эффективности при увеличении фактора в диапазоне от нуля до заданного значения

Если под у понимать не показатель эффективности производ­ства, а производственные затраты на выпуск продукции, то рас­сматриваемое отношение следует интерпретировать как себе­стоимость единицы продукции.

Если — линейная функция, в которой величи-

на интерпретируется как постоянная составляющая затрат, а коэффициент регрессии а_х — как текущий расход на единицу продукции, то себестоимость единицы продукции, рассчитанная по формуле (10.3), будет убывать с ростом производства за счет уменьшения доли постоянных расходов по сравнению с пере­менной составляющей

Коэффициент эластичности

(10.4)

характеризует относительное изменение результата производства на единицу относительного изменения производственного фактора. Численно он равен отношению дополнительного про­дукта данного фактора (предельной производительности) к сред­ней производительности:

Приближенно коэффициент эластичности показывает, на сколько процентов изменяется результат производства при изме­нении /-го фактора на 1 % при неизменной величине других фак­торов.

Предельная норма заменяемости может рассчитываться, когда число факторов более единицы. Здесь необходимо ввести новое понятие — изокванты производственной функции. В общем слу­чае она определяется как поверхность в А'-мерном пространстве производственных факторов на которой показатель эф-

фективности производства постоянен; таким образом, уравнение изокванты имеет вид

Если число факторов равно двум (или когда при К>2 анали­зируются только два фактора то геометрически изокванта может быть изображена как линия на плоскости . Задавая

различные значения константы в уравнении (10.5), можно полу­чить набор изоквант.

Рассмотрим ситуацию, когда все факторы, за исключением двух указанных, фиксированы. В этом случае дифференциал (приращение) определяется соотношением

На изокванте приращениепо определению,

должно быть равно нулю; следовательно,

Преобразовывая это равенство, получим dXi=H_x._Xj(x_h...,x_K)dXj,

где

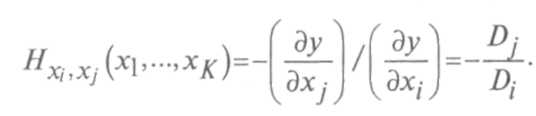
Приближенно коэффициент эластичности показывает, на сколько процентов изменяется результат производства при изме­нении /-го фактора на 1 % при неизменной величине других фак­торов.

Предельная норма заменяемости может рассчитываться, когда число факторов более единицы. Здесь необходимо ввести новое понятие — изокванты производственной функции. В общем слу­чае она определяется как поверхность в А'-мерном пространстве производственных факторов на которой показатель эф-

фективности производства постоянен; таким образом, уравнение изокванты имеет вид

Если число факторов равно двум (или когда при К>2 анали­зируются только два фактора то геометрически изокванта может быть изображена как линия на плоскости . Задавая

различные значения константы в уравнении (10.5), можно полу­чить набор изоквант.

Рассмотрим ситуацию, когда все факторы, за исключением двух указанных, фиксированы. В этом случае дифференциал (приращение) определяется соотношением

На изокванте приращениепо определению,

должно быть равно нулю; следовательно,

Преобразовывая это равенство, получим dXi=H_x._Xj(x_h...,x_K)dXj,где В противном случае (дополнительные продукты имеют разные знаки) предельная норма заменяемости положительна, и, следовательно, для сохранения заданного уровня у рост одного фактора должен сопровождаться ростом другого. Если оба фак­тора являются ресурсами, то положительная норма заменяемости может свидетельствовать либо о грубых нарушениях в организа­ции производства, либо об ошибках в построении производ­ственной функции, например вследствие неверной статистичес­кой обработки выборки при построении уравнения регрессии (на это утверждение также распространяется отмеченное выше ис­ключение). Если же один из факторов — ресурс, а другой количе­ственно характеризует некоторый негативный эффект, например эродированность пашни, то положительная норма заменяемости свидетельствует о «правильном характере» производственной функции. В этом случае увеличение негативного эффекта и дол­жно компенсироваться ростом затрачиваемых ресурсов. Харак­тер изоквант при этом будет таким, как у показанных на рисунке 11, б («возрастающие» линии в плоскости

Помимо изоквант в практике экономического анализа ис­пользуют другие линии — изоклинали. Последние имеет опреде­ленный смысл только в том случае, если предельная норма заме­няемости является переменной величиной. В плоскости изоклиналь определяется уравнением

(10.9)

при фиксированных

Таким образом, изоклиналь — это геометрическое место точек в плоскости в пределах которого норма заменяемости

факторов постоянна. Меняя константу в уравнении (10.9),

можно получить набор изоклиналей.

В заключение (табл. 26—27) приведем расчетные формулы для экономических характеристик производственных функций ос­новных типов. Примеры построения изоквант и изоклиналей приведены в следующем подразделе.

Исключение могут составлять случаи, когда определенный ресурс связан с ка­питальными вложениями, а результирующий показатель оценивается в пределах относительно короткого временного интервала (особенно на начальном отрезке периода окупаемости вложений).

53. Понятие дополнительного продукта фактора и его использования в проектных решениях. Средняя производительность.Дополнительный продукт фактора х (или иначе предельная про­изводительность) определяется частной производной:

причем все остальные факторы считаются постоянными.

По самому смыслу производной ~ она характеризует скорость (темп) изменения показателя эффективности «в данной точке» при изменении фактора и заданных значениях других произ­водственных факторов¹. Приближенно равна приросту Ау про­дукции за счет увеличения фактора на единицу

Если известен дополнительный продукт фактора, то при малых приращениях новое значение показателя эффективно­сти может быть оценено по формуле

(10.2)

Эта формула «предсказывает» линейное изменение показате­ля эффективности при изменении данного фактора, что в общем случае верно лишь при небольших значениях Исключение составляет случай линейной зависимости показателя эффектив­ности от фактора Например, если однофакторная производ­ственная функция линейна: то формула (10.2), с уче­том того что

справедлива при любых значениях В других случаях оценка

¹ По этой причине дополнительный продукт фактора относят к так называе­мым точечным оценкам.

изменения у по формуле (10.2) при больших значениях может приводить к неприемлемо большим погрешностям.

Если известно, что рассматриваемый показатель эффективно­сти у достигает максимума внутри области допустимых значений производственных факторов то максимальное значение

у и соответствующие ему оптимальные значения фактора могут быть определены путем решения системы уравнений:

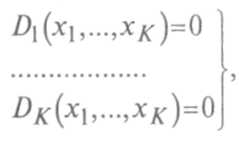
где зависимости предельных продуктов от производственных факторов определяются по формуле (10.1) при заданной зависи­мости

Средняя производительность

(10.3)

отражает средний темп изменения показателя эффективности при увеличении фактора в диапазоне от нуля до заданного значения

Если под у понимать не показатель эффективности производ­ства, а производственные затраты на выпуск продукции, то рас­сматриваемое отношение следует интерпретировать как себе­стоимость единицы продукции.

Если — линейная функция, в которой величи-

на интерпретируется как постоянная составляющая затрат, а коэффициент регрессии а_х — как текущий расход на единицу продукции, то себестоимость единицы продукции, рассчитанная по формуле (10.3), будет убывать с ростом производства за счет уменьшения доли постоянных расходов по сравнению с пере­менной составляющей