51. Оценка значимости представления производственной функции, получаемой по результатам выборочных наблюдений.

Обобщенно задачу, указанную в заголовке данного подразде­ла, можно понимать как оценку соответствия сглаженной зависи­мости используемой в качестве производственной функции, реальной стохастической зависимости результата про­изводства от производственных факторов Частично этот" вопрос мы уже затронули выше, дав содержательную интер­претацию коэффициентов корреляции и корреляционного отно­шения. Рассмотрим теперь его более подробно.

■Анализ выборочных коэффициентов корреляции позволяет сделать некоторые выводы относительно целесообразности ис­пользования сглаженных регрессионных зависимостей результа­та производства у от производственных факторов Снача­ла целесообразно совместно оценить корреляционное отноше­ние R и сводный коэффициент корреляции • Если

(см. приведенную выше градацию тесно­ты связи по значению коэффициента корреляции), констатиру­ется либо отсутствие значимой связи у с либо неполнота исходной информации (малость выборки). В противном случае далее отдельно оценивается коэффициент множественной кор-

реляции Гу_м,„_чХк'

При достаточной его величине (например,

можно предположить, что зависимость у от х_и...,х_к близка к линейной и, следовательно, производственную функцию можно представить в форме линейной регрессии; при

этом, однако, уровень «достаточности» величины опре­деляется чисто произвольно. При промежуточных значениях ко­эффициента корреляции признаком линейного характера регрессии может служить близость значений и

При " использовании приведенных рекомендаций следует учесть, что в случае сравнительно большого числа производ­ственных факторов реальный нелинейный характер влия­ния одного из них на у при расчете коэффициента множествен­ной корреляции может быть замаскирован линейным характером влияния других. В этом случае дополнительную информацию мо­жет дать анализ всей матрицы коэффициентов парной корреля­ции.

Последнее замечание подчеркивает вспомогательный харак­тер рассмотренной процедуры определения допустимого класса функций при построении регрессии у на

Рассмотрим теперь вопрос о степени влияния производственен

ных факторов на результат производства При этом слу-

чайной будем считать только величину а величины х_и...,х_к — неслучайными независимыми переменными.

В математической статистике указанный вопрос решается на основе анализа дисперсий отклонений сглаженных значений

от среднего наблюдаемого а также от-

клонений наблюдаемых величин от сглаженных значений, то есть от линии регрессии

Помимо указанных дисперсий вводится их сумма:

В случае линейной регрессии указанная сумма равна выбороч­ной дисперсии величины у:

По смыслу введенных дисперсий чем больше отношение тем большую роль в изменении наблюдаемых значений у играет зависимость результатов производства от факторов В пределе при то есть при все на-

блюдаемые точки лежат на линии (поверхность) регрессии — от­клонения равны нулю и, значит, линия (поверхность) регрессии полностью описывает зависимость у от x_h...,x_K. В про­тивном случае величина

называемая коэффициентом детерминации, характеризует, какая доля изменений величины у обусловлена изменением факторов Соответственно отношение характери­зует долю изменений величины у, обусловленных действием не­учтенных факторов. Если, например, то говорят, что по­рядка 90 % изменений величины у вызвано изменением произ­водственных факторов а около — влиянием неуч­тенных факторов.

Из определения суммы дисперсий следует, что в случае линейной регрессии коэффициент детерминации равен квадрату

корреляционного отношения, то есть B=R². Более того, можно показать, что в этом случае

где величина формально рассчитывается по соотноше-

нию для выборочного коэффициента множественной корреля­ции, хотя при принятом выше предположении — неслу­чайные независимые переменные) таковым не является.

Сохраняя указанное предположение, рассмотрим вопрос о до­верительных границах, в которых расположены истинные (из ге­неральной совокупности) значения у с учетом разброса наблюда­емых значений у относительно линии регрессии и ошибок опре­деления положения самой линии. Ограничимся случаем линей­ной регрессии для однофакторной зависимости В этом случае доверительные границы для у при заданном уровне доверительной вероятности р определяются соотношением

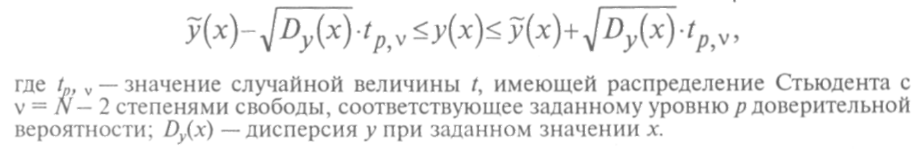
Дисперсия является функцией независимой переменной и определяется соотношением

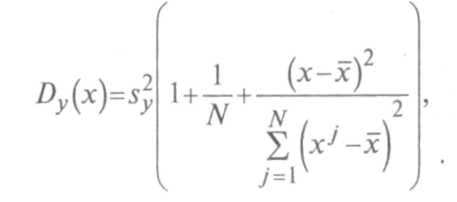
где выборочная оценка sj, дисперсии отклонения случайной не­зависимой величины у от линии регрессии по определению рав­на:

при у^J=a_i+a₂x^J.

Соотношение для дисперсии получено с учетом погрешностей определения коэффициента оепэессии и свободного члена в уравнении регрессии

Для иллюстрации на рисунке 10 показаны доверительные гра­ницы для у при уровне доверительной вероятности пост­роенные по данным задачи 8.1.

Остановимся кратко на проблеме достаточности числа наблю­дений

С формальной точки зрения при построении регрессионной зависимости с М параметрами число на-

блюдений N должно быть не менее М. В противном случае систе­ма нормальных уравнений (при сведении их к линейным алгеб­раическим) будет вырожденной. Таким образом, минимальное ограничение на N таково: Однако с учетом требования

статистической достоверности получаемых результатов ограни­чения на N существенно жестче. Действительно, несмещенная выборочная оценка для дисперсии отклонений случайной вели­чины у от поверхности регрессии определяется соотношением

^у N-M -1.

Следовательно, при дисперсия стремится к бесконечности, что говорит о статистической недостоверности регресси­онной зависимости. Для получения достаточно надежных оценок параметров уравнения регрессии желательно выполнение нера­венства На практике (в случае малых выборок) стре­мятся хотя бы обеспечить выполнение условия