50. Корреляционное отношение. Коэффициент детерминации. Критерии Стьюдента и Фишера, бета-коэффициент.

Как уже отмечалось, коэффициенты корреляции отражают не тесноту связи вообще, а близость этой связи к линей-

ной. Тесноту нелинейных связей можно характеризовать выбороч­ным корреляционным отношением:

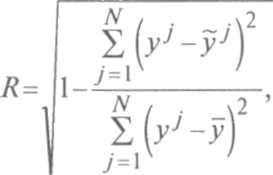
где у¹= f[x{,...,Xx\ — значение результативного показателя, определяемое в соот­ветствии с построенной регрессионной (сглаженной) зависимостью в точках, зада­ваемых анализируемой выборкой.

Область значений корреляционного отношения Корреляционное отношение показывает, насколько принятая

регрессионная зависимость где функция / относится к определенному классу (необязательно линейных функ­ций), соответствует реальной статистической картине.

Для случая линейной регрессии (когда функция / линейна) выполняются соотношения:

Очевидно, что если связь тесная и близкая к линей-

ной, то как будут близки к 1.

Подчеркнем, что хотя в случае линейной регрессии значения коэффициентов совпадают, в общем случае они ха-

рактеризуют различные аспекты исходной статистической ин­формации (выборки), в связи с чем на практике целесообразно совместное их использование.

В про­тивном случае величина

называемая коэффициентом детерминации, характеризует, какая доля изменений величины у обусловлена изменением факторов Соответственно отношение характери­зует долю изменений величины у, обусловленных действием не­учтенных факторов. Если, например, то говорят, что по­рядка 90 % изменений величины у вызвано изменением произ­водственных факторов а около — влиянием неуч­тенных факторов.

Из определения суммы дисперсий следует, что в случае линейной регрессии коэффициент детерминации равен квадрату корреляционного отношения, то есть B=R². Более того, можно показать, что в этом случае

где величина формально рассчитывается по соотношению для выборочного коэффициента множественной корреля­ции, хотя при принятом выше предположении — неслу­чайные независимые переменные) таковым не является.

Коэффициенты корреляции рассчитываются по выборкам и соответственно имеют статистический характер. Фактически они являются функциями случайных величин В связи с этим правомерен вопрос о достоверности расчета коэффициен­тов по приведенным соотношениям. Ниже приводится ряд фор­мул, позволяющих оценить указанную достоверность. Формулы

получены методами математической статистики на основе ряда весьма существенных допущений, основным из которых являет­ся предположение о нормальности частных распределений вели­чин у, х_ь...,х_къ генеральной совокупности. Несмотря на грубость такого допущения в большинстве реальных ситуаций, получае­мые на его основе выводы относительно достоверности выбороч­ных оценок коэффициентов корреляции приемлемы с практи­ческой точки зрения.

Стандартная (среднеквадратическая) ошибка определения вы­борочного значения коэффициента парной корреляции при дос­таточно большой выборке может быть оценена по фор­муле

При малых выборках (Л^< 30)

в случае N > 50

Стандартные ошибки определения коэффициента множе­ственной корреляции и корреляционного отношения R могут быть оценены по формулам

в случае N<30

Значение стандартной ошибки позволяет оценить достовер­ность расчета коэффициентов корреляции. Грубая оценка может быть получена в соответствии с «правилом трех сигм»: если то выборочная оценка коэффициента корреляции при­емлема. Для более полных оценок погрешностей необходим учет закона распределения коэффициентов корреляции.

При больших выборках можно приближенно пола-

гать, что выборочный коэффициент парной корреляции рас­пределен по нормальному закону. При таком предположении доверительный интервал для оценки коэффициента корреляции в генеральной совокупности определяется из соотношения

Величина определяется из уравнения:

(9-2)

Решение уравнения (9.2) находится с помощью таблиц значе­ний функции Лапласа (см. Приложение к данной главе).

Приведенные соотношения могут быть использованы для ориентировочной оценки доверительных интервалов для г₀ в слу­чае а также для грубых оценок доверительных интервалов для сводного коэффициента корреляции и корреляционного от­ношения из генеральной совокупности.

Для некоторых частных случаев могут быть получены более точные соотношения.

При малом объеме выборки и достаточно сильной

корреляции закон распределения выборочного коэффи-

циента парной корреляции существенно отличается от нормаль­ного. В этом случае может быть использована статистика вида

Р. Фишером установлено, что статистика Z подчиняется зако­ну, близкому к нормальному, со следующими параметрами: математическое ожидание:

дисперсия:

учетом сказанного доверительный интервал для коэффици­ента определяется из соотношения

Помимо приведенных выше соотношений для определения доверительного интервала, с вероятностью р содержащего значе­ние коэффициента корреляции из генеральной совокупности, в математической статистике выведены формулы для проверки значимости тех или иных гипотез.

Например, для проверки гипотезы о коэффициенте парной корреляции (то есть предположения о том, что коэффи-

циент корреляции из генеральной совокупности с доверитель­ной вероятностью не отличается значимо от нуля) в случае большого объема выборки используется критерий

вида

где имеет тот же смысл, что и в соотношении (9.2).

При выполнении неравенства сформулированная гипотеза считается верной. В противном случае она отвергается, то есть считается, что коэффициент корреляции значимо отличается от нуля.

При объеме выборки для проверки той же гипотезы

статистика