49. Понятие функциональной и корреляционной зависимости между результатами и факторами производства. Коэффициент парной, множественной корреляции.

В качестве одной из указанных характеристик может исполь­зоваться коэффициент корреляции, показывающий, насколько за­висимость, выраженная выборкой, близка к линейной.

Как было принято ранее, результативный показатель и произ­водственные факторы рассматриваются в качестве случайных ве­личин. В то же время законы распределения этих величин неиз­вестны. Следовательно, при определении всех характеристик, в том числе и коэффициентов корреляции, мы будем оперировать соответствующими выборками.

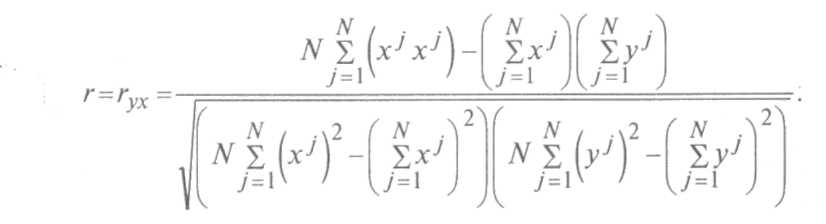
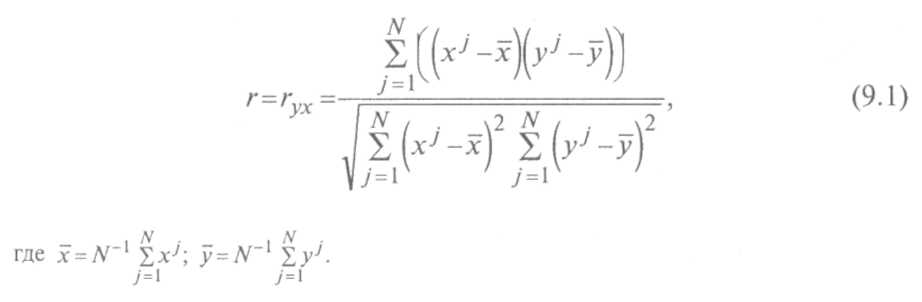
Для расчетов более удобна следующая формула, полученная преобразованием предыдущей:

Для парной (однофакторной) зависимости (К= 1) выборочное значение коэффициента парной корреляции по определению за­дается соотношением

В геометрической интерпретации коэффициент г показывает, насколько геометрическое место точек, определяемое выборкой, близко к прямой линии. Подчеркнем это обстоятельство еще раз: величина коэффициента корреляции отражает не тесноту связи у и х вообще, а только близость этой связи с линейной. Далее будут приведены примеры, когда коэффициент корреляции по абсо­лютной величине мал (линейная связь слабая), а реальная связь результата производства с производственными факторами доста­точно тесна.

В соответствии с определением коэффициента парной кор­реляции его значения находятся в интервале На прак­тике принято считать, что если модуль коэффициента нахо-

дится в пределах то линейная связь отсутствует. При

связь плохая, при — слабая, при — умеренная, при -средняя, при

— высокая, при —очень высокая, при

— полная. При положительных значениях коэффи- циента парной корреляции говорят о прямой связи, при отрица- тельных — об обратной.

В случае, когда мы имеем дело с множественной зависимос­тью ( ), используют коэффициенты парной корреляции для пар отдельных факторов— и т.д., которые отражают кор-

релированность соответствующих факторов (но только в смысле линейной связи!). Формула для выборочных оценок таких коэф­фициентов подобна (9.1).

Введем матрицу коэффициентов парной корреляции:

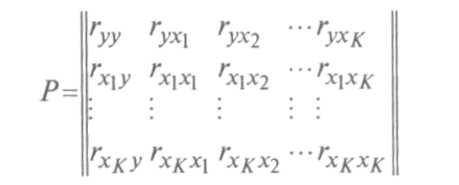
Тогда коэффициент множественной корреляции (иногда ис­пользуют термин «свободный коэффициент корреляции») между у и совокупностью факторов определяется следующим

образом:

где Р— определитель матрицы Р; Руу — алгебраическое дополнение первого эле­мента матрицы Р.

Область значений коэффициента множественной коооеляции. Этот коэффициент показывает, насколько в

мерном пространстве переменных геометрическое место точек, определяемое выборкой, близко к гиперплоскости.

В случае парной зависимости формула для коэффициента множественной корреляции сводится к (9.1), а в случае зависи­мости результата производства от двух факторов может быть пре­образована к виду