44. Виды и способы представления производственных функций и их использование для определения оптимальных размеров факторов.

Произв функция- математически выраженная зависимость результатов про-ва от произв факторов.у=у(х,х,х,…) их виды:

Тип произ-ой фун-ии	Вид урав-я у=f(x)
Линейная Степенная Гиперболическая Параболическая Кинетическая Асимптотического роста

Способы: Табличный используют при изучении зависимостей по наблюдениям, графический нагляден но несколько неточен используется для опр характера изменения показателей, аналитический(уравнение), номографический(номограммы)для быстрого определения значений произв функций и реализации аналитических форм связи между переменными без высокой точности.

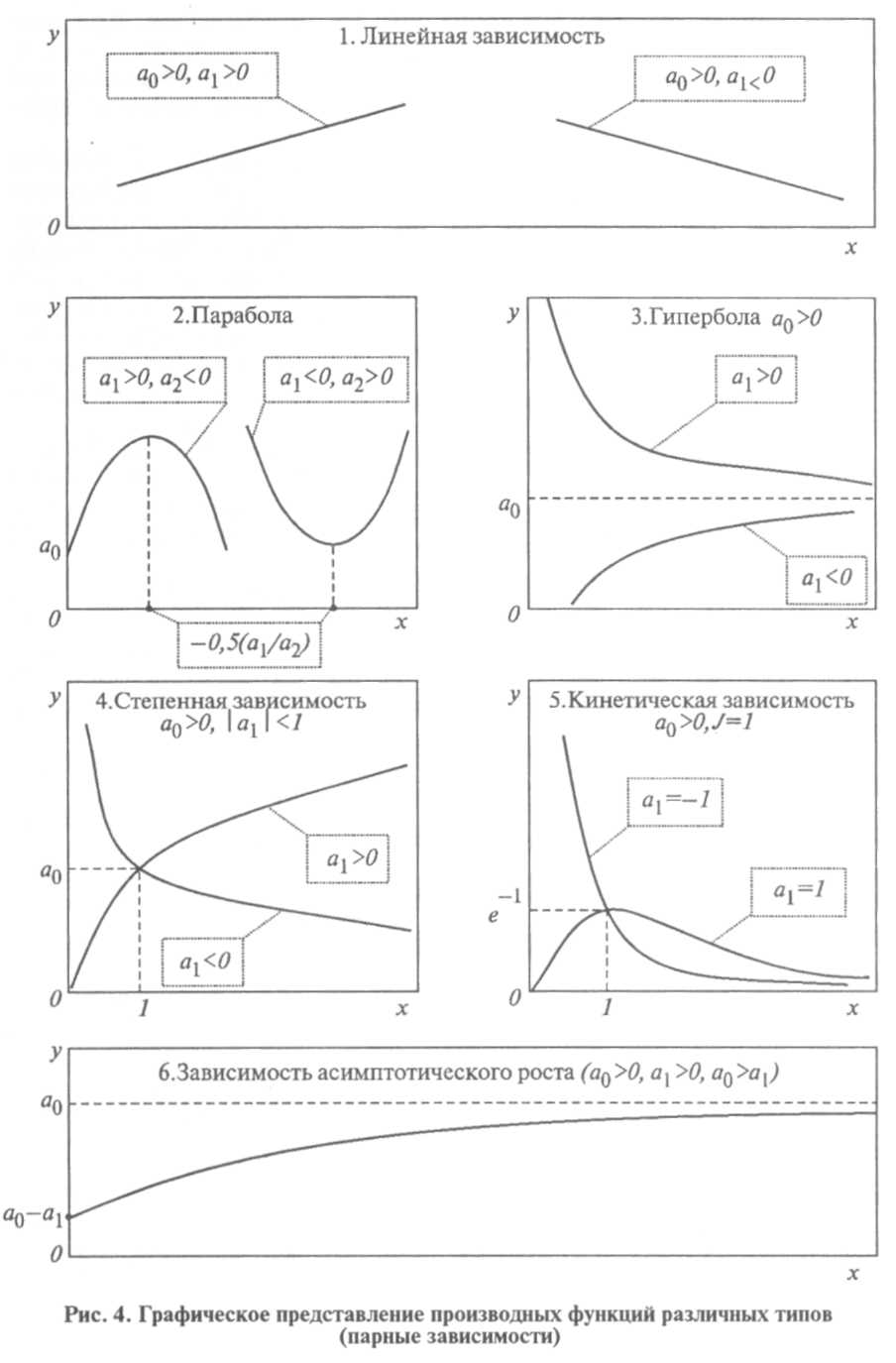
45. Графическое представление производственных функций различных видов парной зависимости.

Графическое изображение основных видов парных математи­ческих зависимостей приведено на рисунке 4.

Линейная зависимость применяется в случае равномерного нарастания (убывания) результативного признака с изменением значения данного фактора производства. Линейные парные и множественные зависимости используются в землеустройстве для моделирования нормальной урожайности сельскохозяй­ственных культур при проведении земельно-оценочных работ. В модель включают различные факторы и условия производства (климатические характеристики, качество почв, количество вно­симых удобрений и т. д.).

Часто линейные производственные функции применяются также при анализе использования земель в конкретных сельско­хозяйственных предприятиях с целью выявления основных фак­торов, влияющих на эффективность производства. Эти же функ­ции используются при планировании урожайности сельскохо­зяйственных культур в схемах и проектах землеустройства.

Степенная зависимость может быть использована в случае криволинейного возрастания (убывания) результативного пока­зателя при изменении фактора производства. Такие зависимости широко применяются для анализа уровня и интенсивности ис­пользования земель в районах со сложными природными усло­виями: в зонах орошаемого земледелия, в хозяйствах с развитой водной эрозией почв и дефляцией, в районах широкого проведе­ния осушительных мелиорации и культуртехнических мероприя­тий.

Гиперболическая зависимость необходима при изучении об­ратно пропорциональных связей, когда увеличение факторного показателя (в области неотрицательных значений) приводит к уменьшению результата. В землеустройстве такие модели нахо­дят широкое применение при определении различных нормати­вов, прежде всего при расчете удельных затрат на строительство населенных пунктов на 1 жителя в зависимости от крупности по­селений, затрат на строительство животноводческих комплексов и ферм в расчете на 1 голову скота при различной концентрации поголовья, удельных затрат на 1 га осваиваемой или мелиорируе­мой площади земель в зависимости от размера объекта мелиора­ции и т. д.

При экономическом обосновании проектных землеустрои­тельных решений гиперболические зависимости используются для определения затрат на холостые повороты и заезды сельско хозяйственной техники в зависимости от длины полей, при рас­чете простоев техники по организационным и техническим при­чинам в зависимости от площади полей и рабочих участков, при анализе влияния концентрации посевов на себестоимость про­дукции растениеводства и т. д.

Полиномиальная зависимость (главным образом уравнение параболы второго порядка) используется в случае ускоренного возрастания (убывания) результативного показателя при равно­мерном изменении фактора производства. Иногда такая зависи­мость нужна ввиду наличия максимума (минимума) результата производства (у) в границах изменения производственного фак­тора (х). Так бывает, в частности, при поиске оптимальных пло­щадей различных земельных участков (землевладений и земле­пользовании, полей, рабочих и бригадных участков, севооборо­тов, сенокосо- и пастбищеоборотов).

Например, если найдена параболическая зависимость стоимо­сти валовой продукции от размера землевладения, из нее можно определить площадь сельскохозяйственного предприятия, при которой стоимость валовой продукции (или прибыль) достигает максимума.

Кинетическая зависимость и уравнение асимптотического ро­ста применяются при проведении землеустройства для анализа уровня интенсивности использования земель и расчета различ­ных нормативных показателей. Так, кинетическая зависимость может быть использована для оценки целесообразности укрупне­ния или разукрупнения хозяйств, а уравнение асимптотического роста — для установления зависимости чистого дохода, получае­мого от агроклиматического воздействия лесополос (у), от высо­ты насаждений (х).

Приведенный список уравнений связи не является исчерпы­вающим; при проведении землеустройства иногда применяются и другие виды производственных функций.

хозяйственной техники в зависимости от длины полей, при рас­чете простоев техники по организационным и техническим при­чинам в зависимости от площади полей и рабочих участков, при анализе влияния концентрации посевов на себестоимость про­дукции растениеводства и т. д.

Полиномиальная зависимость (главным образом уравнение параболы второго порядка) используется в случае ускоренного возрастания (убывания) результативного показателя при равно­мерном изменении фактора производства. Иногда такая зависи­мость нужна ввиду наличия максимума (минимума) результата производства (у) в границах изменения производственного фак­тора (х). Так бывает, в частности, при поиске оптимальных пло­щадей различных земельных участков (землевладений и земле­пользовании, полей, рабочих и бригадных участков, севооборо­тов, сенокосо- и пастбищеоборотов).

Например, если найдена параболическая зависимость стоимо­сти валовой продукции от размера землевладения, из нее можно определить площадь сельскохозяйственного предприятия, при которой стоимость валовой продукции (или прибыль) достигает максимума.

Кинетическая зависимость и уравнение асимптотического ро­ста применяются при проведении землеустройства для анализа уровня интенсивности использования земель и расчета различ­ных нормативных показателей. Так, кинетическая зависимость может быть использована для оценки целесообразности укрупне­ния или разукрупнения хозяйств, а уравнение асимптотического роста — для установления зависимости чистого дохода, получае­мого от агроклиматического воздействия лесополос (у), от высо­ты насаждений (х).

Приведенный список уравнений связи не является исчерпы­вающим; при проведении землеустройства иногда применяются и другие виды производственных функций.

хозяйственной техники в зависимости от длины полей, при рас­чете простоев техники по организационным и техническим при­чинам в зависимости от площади полей и рабочих участков, при анализе влияния концентрации посевов на себестоимость про­дукции растениеводства и т. д.

Полиномиальная зависимость (главным образом уравнение параболы второго порядка) используется в случае ускоренного возрастания (убывания) результативного показателя при равно­мерном изменении фактора производства. Иногда такая зависи­мость нужна ввиду наличия максимума (минимума) результата производства (у) в границах изменения производственного фак­тора (х). Так бывает, в частности, при поиске оптимальных пло­щадей различных земельных участков (землевладений и земле­пользовании, полей, рабочих и бригадных участков, севооборо­тов, сенокосо- и пастбищеоборотов).

Например, если найдена параболическая зависимость стоимо­сти валовой продукции от размера землевладения, из нее можно определить площадь сельскохозяйственного предприятия, при которой стоимость валовой продукции (или прибыль) достигает максимума.

Кинетическая зависимость и уравнение асимптотического ро­ста применяются при проведении землеустройства для анализа уровня интенсивности использования земель и расчета различ­ных нормативных показателей. Так, кинетическая зависимость может быть использована для оценки целесообразности укрупне­ния или разукрупнения хозяйств, а уравнение асимптотического роста — для установления зависимости чистого дохода, получае­мого от агроклиматического воздействия лесополос (у), от высо­ты насаждений (х).

Приведенный список уравнений связи не является исчерпы­вающим; при проведении землеустройства иногда применяются и другие виды производственных функций.

хозяйственной техники в зависимости от длины полей, при рас­чете простоев техники по организационным и техническим при­чинам в зависимости от площади полей и рабочих участков, при анализе влияния концентрации посевов на себестоимость про­дукции растениеводства и т. д.

Полиномиальная зависимость (главным образом уравнение параболы второго порядка) используется в случае ускоренного возрастания (убывания) результативного показателя при равно­мерном изменении фактора производства. Иногда такая зависи­мость нужна ввиду наличия максимума (минимума) результата производства (у) в границах изменения производственного фак­тора (х). Так бывает, в частности, при поиске оптимальных пло­щадей различных земельных участков (землевладений и земле­пользовании, полей, рабочих и бригадных участков, севооборо­тов, сенокосо- и пастбищеоборотов).

Например, если найдена параболическая зависимость стоимо­сти валовой продукции от размера землевладения, из нее можно определить площадь сельскохозяйственного предприятия, при которой стоимость валовой продукции (или прибыль) достигает максимума.

Кинетическая зависимость и уравнение асимптотического ро­ста применяются при проведении землеустройства для анализа уровня интенсивности использования земель и расчета различ­ных нормативных показателей. Так, кинетическая зависимость может быть использована для оценки целесообразности укрупне­ния или разукрупнения хозяйств, а уравнение асимптотического роста — для установления зависимости чистого дохода, получае­мого от агроклиматического воздействия лесополос (у), от высо­ты насаждений (х).

Приведенный список уравнений связи не является исчерпы­вающим; при проведении землеустройства иногда применяются и другие виды производственных функций.