7.Повторение испытаний. Схема Бернулли. Биномиальное распределение. Формула Пуассона

Последовательные испытания наз-ся независимыми, если вероятность осущ-я любого исхода в n-ом по счету эксперименте не зависит от исходов предыдущих испытаний.

Схема испытаний Бернулли:

1. послед-ть независимых испытаний с двумя исходами («успех» и «неуспех»);

2. эксперимент проводится n раз в неизменных усл-ях, т.е. вероятности «успеха»(p) и «неуспеха»(1-p=q) неизменны.

n-число испытаний, k-число благоприятных исходов, событие А – «успех», Х – случ.величина, обозначающая число «успехов» в n испытаниях по сх. Бернулли (Х=0,1,2,…n).

- формула Бернулли, где C_n^k-число случайного размещения события А в послед-ти из n мест.

Соответствующее распр-е случ.вел.Х наз-ся биномиальным распр-ем. Свойства бином.распр-я:

1. ;

2. -матем.ожидание

3. -дисперсия.

Приближенная формула Пуассона: . При , при условии (-интенсивность потока): = = ; .

• 9.Производящие функции вероятностей.

• G(z)=P₀+P₁z+P₂z+…+P_kz^k…=M[z^k]

• G(1)= (кси) =1

• G’(z)=P₁+2P₂z+3P₃z²+…+ KP_Kz^k-1

• G’(1)=M[x]=m

• G”(z)=2P₂+6P₃z+…+k(k-1)P_kZ^k-2

• G”(1)=∑k²P_k - ∑kP_k

• _{k=0 k=0}Биномиальное распределение

• X=0,1,2,…n –бином-ое распредел.

• Pk=P[x=k]=C^k_nP^kq^n-k

• G(z)=P₀+P₁z+P₂z+…+P_kz^k…=∑ C^k_nP^kq^n-kz^k=

• =∑ C^k_n(pz)^kq^n-k=(pz+q)ⁿ

• G’(z)=n(pz+q)^n-1p

• G’(1)=M[x]=np

• G”(z)=n(n-1)( pz+q)^n-2p²

• G”(1)=n(n-1)p²

• M[x]=np = ∑kP_k D[x]=npq = ∑(k-np)²P_k

• Распределение Пуассона

• P_k=P[x=k]= (λ^k\k!)e^-λ

• G(z)= ∑(λ^k\k!)e^-λz^k=e^-λ∑( λz)^k\k!= e^-λ e^zλ= e^λ(z-1)

• G’(1)= e^λ(z-1) λ

• G’(1)= λ= M[x]=m

• G”(z)= e^λ(z-1) λ²

• G”(1)= λ²

• M[x]=λ D[x]= λ²+ λ- λ²= λ

• Геометрическое распределение

• X=0,1,2….

• P_k=P[x=k]q^kp

• G(z)= ∑P_kz^k=∑q^kpz^k=p∑(qz)^k=P*1\(1-qz)=P\(1-qz)

• M[x]=1\p D[x]=q\p²

• 10.Вероятность в непрерывных пространствах элементарных событий и ее свойства. Геометрические вероятности

• Пусть - непрерывное простр-во.

• Алгебра событий (F) – это система подмножеств , кот.удовл-ет следующим свойствам:

• 1. ;

• 2. A,B F => A+B F, AB F, не А и не В CF;

• 3 . F явл-ся сигма-алгеброй, если определены операции.

• Пусть событие А F, тогда Р(А) – вероятность, число, которое должно удовл-ть: 1. Р(А)>=0; 2. P( )=1; 3. A+B F => P(A+B)=P(A)+P(B). Свойства вероятностей:

• 1. - вер-ть невозможного события

• 2.

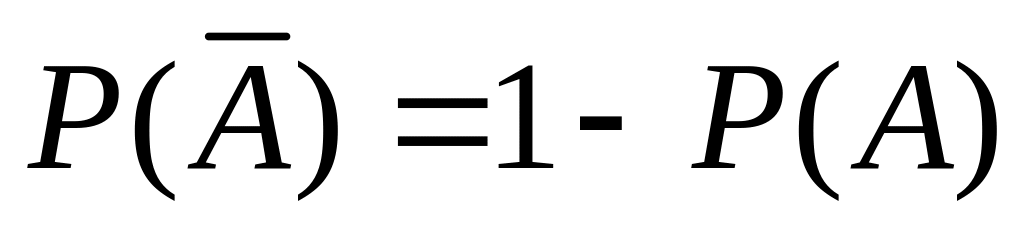
• 3. - если А-следствие В, то Р(А)<=Р(В).

• 4. P(A+B)<=P(A)+P(B)

• 5. непрерывности:

• если А1, А2,…, Аn,…: , то ;

• если , то .

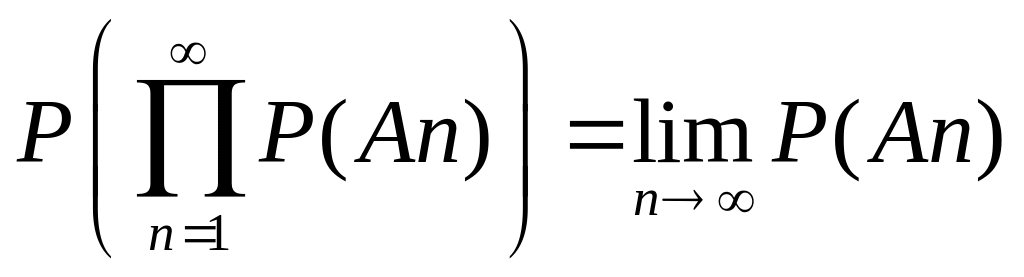• Геометрические вер-ти, Для любого подмножества А можно посчитать его площадь: Р(А)=площ.А/площ.

• Т.к. вер-ть пропорцион-на площади, то чем > лощадь, тем > вероятность попадания в событие.

• P(A)=mes(A)/mes( ) – мера А/мераS.

11.Непрерывные случайные величины. Функция распределения и плотность распределения, и их Свойства. Механическая интерпретация. Свойства мат. Ожидания и дисперсии. Квантили. Мода. Медиана. Асимметрия и эксцессСлучайная величина Х называется непрерывной, если для нее существует неотрицательная частично-непрерывная функция f(x) , удовлетворяющая для любых значений x равенству (случайные величины, возможные значения которых образуют некоторый интервал). f_x - плотность распределения вероятностей (плотность распр-я единичной массы на инт-ле). Св-ва:

е сли x [a;b]: 1. f(x)>=0; 2. ; ;

е сли : 1. f(x)>=0; 2. ; - норм.распр-е.

F(x) – ф-я распределения для непрер.случ.величин, определена на всей числовой оси, ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х. Свойства:

1. 0 <=F(X)<= 1

2. F(- )=0

3. F(+ )=1

4. F(X)-неубыв.ф-я

6. F(X)=dF(X)/dx

7. - вер-ть попадания в отрезок [c;d].

Мат.ожидание: , , где f(x)dx=P[x<X<x+dx] – элемент вер-ти. Свойства:

1. M[cX]=cM[X]

2. M[c+X]=c+M[X]

3. M[X+Y]=M[X]+M[Y]

4. = ,

Дисперсия: , .Начальный момент k-го порядка - ;

Центральный момент k-го порядка - .Асимметрия - , где - ср.квадратич.отклонение

Эксцесс – хар-ет форму распред-я в окрестности вершины

К вантиль – абсцисса (точка на оси х), которая слева от себя отделяет площадь под графиком плотности, равную Р. F(x_p)=P – порядок квантили. 1. ; 2. . Квантиль порядка 0,5 – х_0,5 – для любого распр-я наз-ся медианой (h) (отделяет ½ площади под плотностью слева и справа). Если распр-е симметрично, то h совпадает с мат.ож. m.

М ода (d) – абсцисса, при кот. плотность распр-я имеет максимум: f(d)=max

- моды нет (несколько лок.максимумов)

12. Нормальное распределение. Вероятность попадания в интервал, симметричный относительно мат. ожидания. Асимметрия и эксцесс распределения. Вычисление центрального момента порядка k. Стандартизированное нормальное распределение и его свойство. Правило трех сигм.

Нормальное распределение N(m,²) имеет плотность, определяемую формулой:

Функция распр-я F(х) норм.распр-я равна:

Параметры m и ² норм.распр-я равны соответственно мат.ожиданию и дисперсии случ.вел-ны Х:

Центральные моменты норм.распр-я можно вычислить из рекуррентного ур-ния:

μ_k+2=(k+1)²μ_k , k=0,1,2,… (причем μ₀=1)

Для норм.распр-я все центр.моменты нечетного порядка равны 0.

Коэффициент ассиметрии a_x норм.распр-я равен 0.

a_x=μ₃/₃

Из формул получаем: μ₂=², μ₄=3⁴

Коэффициент эксцесса равен 0: е_х= μ₄/⁴-3=0

Стандартизированное нормальное распределение и его свойство.

Норм.распр-е с нулевым мат.ожиданием и дисперсией,равной 1, назыв.стандартным норм.распр-нием:

Х N(0,1)

Ф-ла плотности (х) станд.норм.закона равна

, -<x<

А функция распр-я:

Так как плотность распр-я станд.норм.закона (х) симметрична относ-но оси ординат,то для ф-ции распр-я Ф(х) справедливо след.св-во: Ф(-х)=1-Ф(х)

Зн-я функции Ф(х) использ.при вычислении вер-ти попадания норм.распр-ной случ.величины Х в заданный интервал:

В практич.задач часто приходится вычислять вер-ть попадания случайной величины Х N(m,²) в интервал, симметричный относительно ее математического ожидания m:

Используя получ.рез-тат,вычислим вер-ть отклоенения от мат.ожидания норма.распр-ной случ.вел-ны на вел-ну,равную трем средневкадратич.отклонениям, 3:

P[|X-m|<3]=2Ф(3)-12*0,9987-10,9973

Этот результат известен как «правило трех сигм»: с вер-тью 0,9974(практически =1)зн-е нормально распределенной случ.вел-ны лежит в интервале (m-3;m+3)

Правило трех сигм это правило часто используется для подтверждения или отбрасывания гипотезы о нормальном распределении случайной величины.