24.Проверка гипотез о равенстве дисперсий и средних.

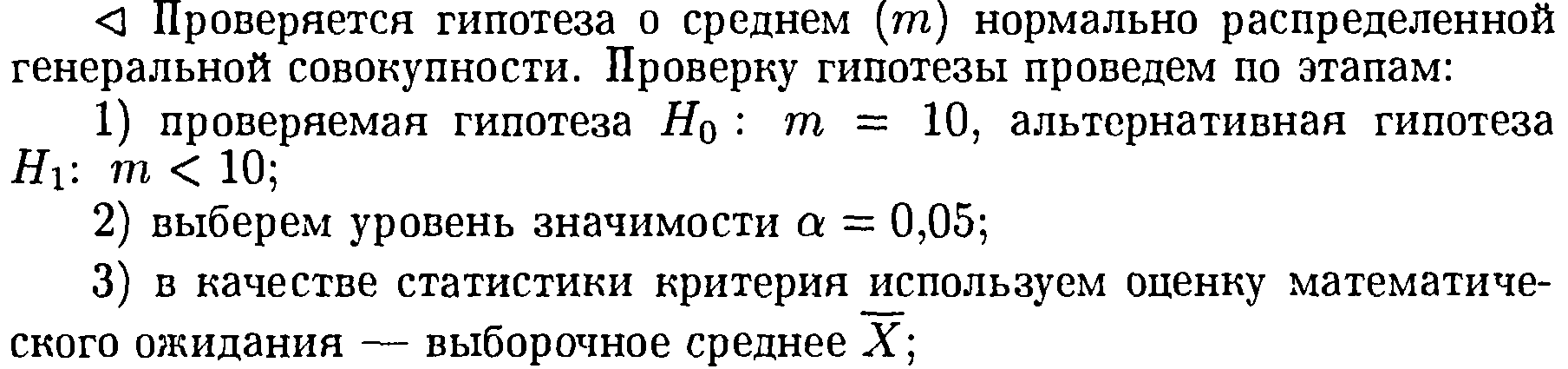
4)так как выборка получена из нормально распределенной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией При условии, что верна гипотеза Н₀, мат. ожидание этого распределения равно 10. Нормированная статистика имеет нормальное распределение N (0,1).

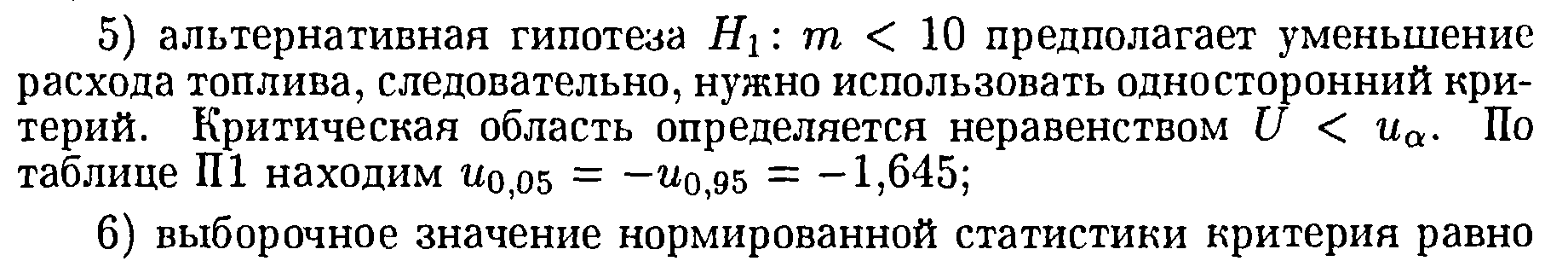
25. Регрессионный анализ. Оценки параметров линейной регрессии методом наименьших квадратов.

Зависимая переменная Y. Факторы, влияющие на Y – независимые переменные х₁, х₂, х_k. Y=f(x₁,х₂, х₃,х₄) + ε. Случайная ошибка – ε.

Уравнение множественной регрессии:

β – параметры. Коэффициент корреляции . Ковариации: Если X и Y независимы, cov (X;Y)=0, обратное не верно. Коэффициент ковариации показывает степень линейной зависимости между X и Y. Если коэффициент ковариации равен 0, то зависимости нет.

Числовые характеристики двух случайных величин:

1. M [X + Y] = M [X]+ M[Y]

2. D [X+Y] = D [X] + D [Y] + 2 cov (X;Y)

3. D [X-Y] = D [X]+D[(-Y)]+2 cov (X;Y)= D [X] + D [Y] - 2 cov (X;Y)

4. Если X и Y независимы, то cov (X;Y)=0, следовательно D [X+Y]=D [X]+ D [Y]

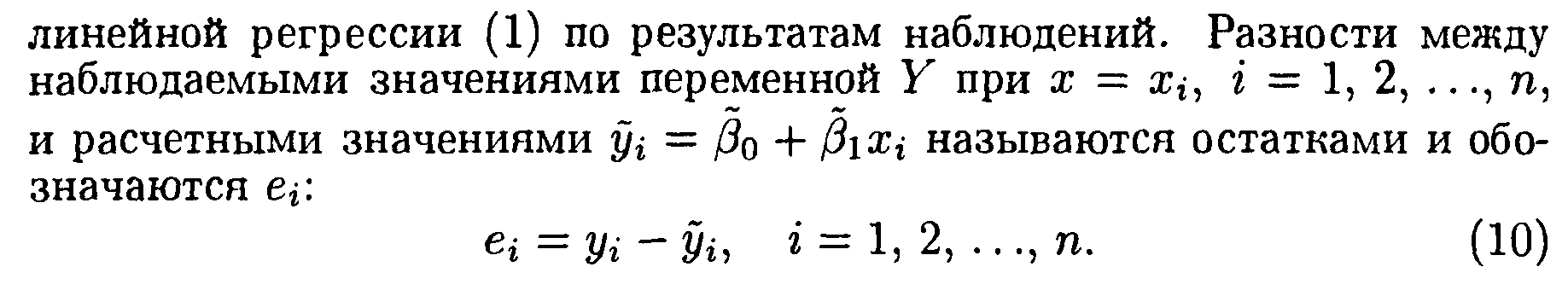
26. Анализ значимости и адекватности регрессионной модели.