Скругление углов

Скругление прямого угла

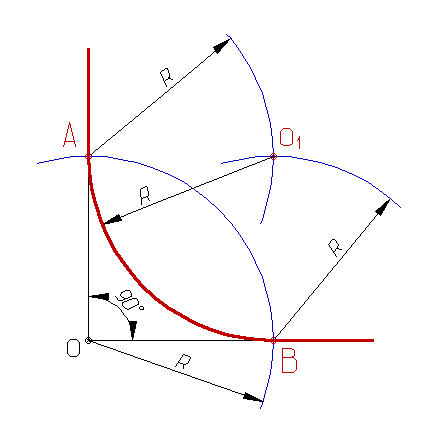
Cкругление прямого угла, имеющего вершину О, дугой радиуса R осуществляется в следующей последовательности:

1. Из вершины О проводят дугу заданным радиусом R, до пересечения со сторонами угла в точках А и В (точки сопряжения);

2. Центр скругления О₁ должен находится на геометрическом месте точек, равноудаленных от сторон угла, т.е. на биссектрисе угла АОВ и определяется точкой пересечения дуг радиуса R, проведенных из точек сопряжения А и В;

3. Проводят дугу АВ  радиусом R и центром О₁.

Скругление острого угла

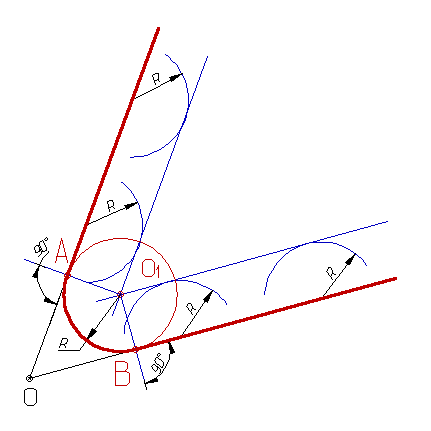
Скругление острого угла дугой радиуса R можно выполнить в следующей последовательности:

1. Геометрическим местом точек, равноудаленных от сторон угла, будут являться прямые, параллельные сторонам угла и проходящие от них на расстоянии R;

2. Точка пересечение этих прямых определяет центр скругления О₁;

3. Пересечение перпендикуляров опущенных из центра скругления  со сторонами определят положение точек сопряжения А и В;

4. Поводим дугу АВ из центра О₁ радиусом R.

Скругление тупого угла

Скругление тупого угла производится точно так же, как и острого. Можно несколько изменить ход построения, если воспользоваться биссектрисой угла:

1. Строят биссектрису угла;

2. Проводят прямую, параллельную одной из сторон угла и отстоящую от нее на расстоянии R;

3. Точка пересечения этой прямой с биссектрисой определяет положение центра скругления О₁;

4. Пересечение перпендикуляров опущенных из центра скругления  со сторонами определят положение точек сопряжения А и В;

5. Поводим дугу АВ из центра О₁ радиусом R.

Внешнее сопряжение прямой линии с дугой

Сопряжение дуги окружности радиуса R с прямой, заданной отрезком АВ, дугой радиусом r выполняется в следующей последовательности:

1. Находим центр сопряжения - точку О₁, как точку пересечения прямой параллельной АВ и отстоящей от нее на расстоянии r и дуги  окружности радиуса R+ r, концентричной заданной;

2. Опускаем перпендикуляр из точки О₁ на прямую АВ. Основание перпендикуляра - точка D - точка сопряжения;

3. Соединяем прямой центр окружности О с центром сопряжения О₁, которая пересекая заданную окружность, определит положение второй точки сопряжения Е.

Внутреннее сопряжение прямой линии с дугой

Сопряжение дуги окружности радиуса R с прямой, заданной отрезком АВ, дугой радиусом r выполняется в следующей последовательности:

1. Находим центр сопряжения - точку О₁, как точку пересечения прямой параллельной АВ и отстоящей от нее на расстоянии r и дуги  окружности радиуса R- r, концентричной заданной;

2. Опускаем перпендикуляр из точки О₁ на прямую АВ. Основание перпендикуляра - точка D - точка сопряжения;

3. Соединяем прямой центр окружности О с центром сопряжения О₁, которая пересекая заданную окружность, определит положение второй точки сопряжения Е.

Сопряжение дуг с дугами

Внешнее сопряжение дуг

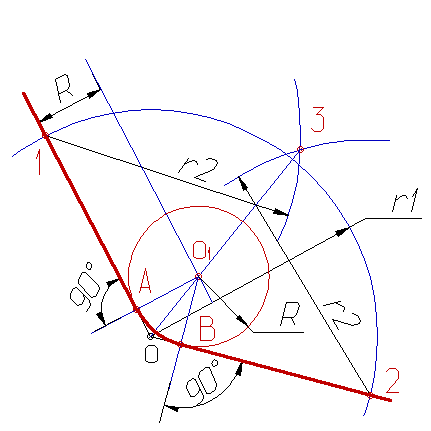
При внешнем сопряжении центры О₁ и О₂ сопрягаемых дуг радиусов R₁ и R₂ лежат вне сопрягающей дуги радиуса R.

Внешнее сопряжение дуг выполняется в следующей последовательности:

1. Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R₁+R  и R₂+R соответственно концентричных окружностям с радиусами R₁ и R₂;

2. Соединяем прямыми центр сопряжения О с центрами окружностей О₁ и О₂, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;

3. Строят сопряжение.

Внутреннее сопряжение дуг

При внутреннем сопряжении центры О₁ и О₂ сопрягаемых дуг радиусов R₁ и R₂ лежат внутри сопрягающей дуги радиуса R.

Внутреннее сопряжение дуг выполняется в следующей последовательности:

1. Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R-R₁  и R-R₂ соответственно концентричных окружностям с радиусами R₁ и R₂;

2. Соединяем прямыми центр сопряжения О с центрами окружностей О₁ и О₂, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;

3. Строят сопряжение.

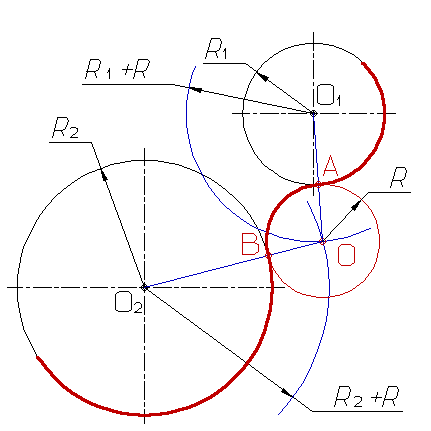
Смешанное сопряжение дуг

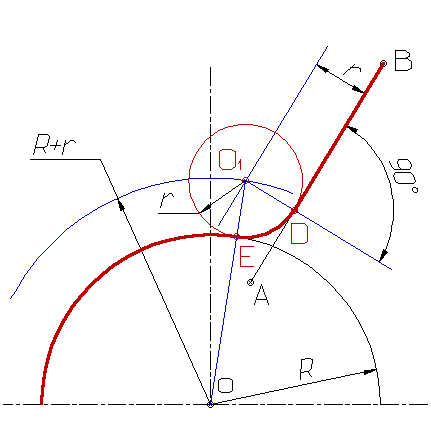
При смешанном сопряжении центр О₂ одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О₁ другой сопрягаемой дуги вне ее.

Внутреннее сопряжение дуг выполняется в следующей последовательности:

1. Находим центр сопряжения, точку О пересечения дуг окружностей с радиусами R+R₁  и R-R₂ соответственно концентричных окружностям с радиусами R₁ и R₂;

2. Соединяем прямыми центр сопряжения О с центрами окружностей О₁ и О₂, которые пересекаясь с заданными окружностями определяют положение точек сопряжения А и В;

3. Строят сопряжение.

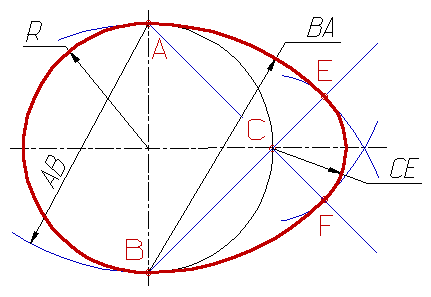
Овал с двумя осями симметрии

Строят овал обычно по осям АВ и СД в следующей последовательности:

1. Соединим прямой линией точки А и С;

2. Радиусом большой полуоси АО засекают продолжение малой оси СD в точке Е;

3. Радиусом СЕ (разность полуосей) засекают линию АС в точке F;

4. Проводят перпендикуляр через середину отрезка АF, он пересекает оси овала в точках 1 и 2, которые являются искомыми центрами дуг окружностей;

5. Центры 3 и 4 находят как точки симметричные центрам 1 и 2;

6. Точки сопряжения К, L, M, и N находятся на линиях центров соответственно 2-1, 2-3, 4-3 и 4-1.

7. Строят овал как последовательность дуг окружностей: первая с центром 1 и радиусом А1, вторая с центром 2 и радиусом С2, третья с центром 3 и радиусом В3, четвертая с центром 4 и радиусом D4.

Овал с одной осью симметрии

Овал с одной осью симметрии называется овоидом (яйцевидный овал) Его задают обычно радиусом или диаметром основной окружности.

Построение овоида производится в следующей последовательности:

1. Проводят линии центров АС и ВС;

2. Радиусом АВ, равным диаметру заданной окружности, проводят дугу BF до линии центров АС, а радиусом ВА - дугу АЕ до линии центров ВС;

3. Замыкают овал дугой EF из центра С.