2 Алгоритм оценки координат при известном изображении фона объекта. Критерий максимума апостериорной плотности

Далее рассмотрим подход, состоящий в том, что будем «отдельно» решать задачу определения координат объекта на изображении и задачу прогнозирования местоположения объекта в будущем кадре (задача планирования следующего наблюдения L_n).

1-ое слагаем.-показатель прогнозируемой гауссовой плотности, 2-ое – прогнозируемое условное распределение.

Таким образом, задача нахождения λ_h(n) сводится к поиску глобального минимума J в пространстве параметров [λ_hx(n) λ_hy(n)], причем первая составляющая критерия (5.22) выступает по существу в роли штрафной функции, задающей свойства зоны поиска. Процедура поиска заключается в перемещении изображения некоторого эталонного объекта по изображению фона и вычислении для каждого положения объекта значения критерия.

В общем случае, критерий (5.22) является многоэкстремальным, поэтому целесообразно делать полный перебор.

Целесообразно исследовать не все изображение L_n, а только зону в районе точки прогноза, определяемой дисперсиями D_hx(n), D_hy(n). Результаты поиска по (5.22) являются измерениями ………………..( -математическое ожидание, -оценка).

Уравнение (5.23) – уравнение наблюдения (измерения), линейное.

Алгоритм оптимальной оценки вектора Λ_h представляет собой фильтр Калмана. Фильтр Калмана – тот же наблюдатель состояния, но при наличии помех:

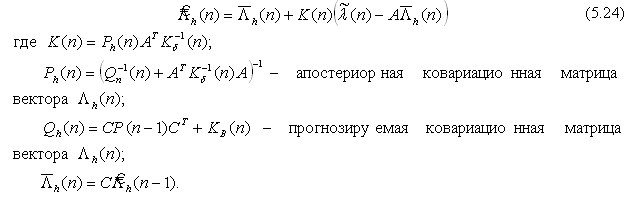
Из матрицы Q_h(n) легко получить матрицу K_h(n), из вектора …………………..

Фильтр Калмана устроен так, что если бы в модели (5.13) отсутствовал шум, то коэффициент K(n)→0 и тогда в качестве оценки всегда был бы прогноз.

Билет 13

1 Методы сегментации, дискриминантный критерий.

Сегментация изображения – это разделение изображения на сегменты, то есть на совокупность областей. При этом предполагается, что точки каждой из смысловых областей обладают некоторой степенью общности, которая позволяет их рассматривать как одну область.

Например, ведется съемка поверхности Земли и возникает необходимость выделения точек, принадлежащих дорогам, рекам, полям и т.д. При распознавании текста выделяют точки, принадлежащие буквам, символам. Часто требуется выделить на изображении точки, принадлежащие, например, движущимся объектам. Совокупность этих точек является сегментом.

Сегментация подразумевает разделение всех точек изображения на какое-то количество непересекающихся множеств. Эти множества могут называться классами, а сам процесс классификацией. Сегментация может выполняться как по отдельному изображению, так и по последовательности. В общем случае это пространственная временная обработка изображения.

Сегментация достаточно сложная задача, часто не имеющая однозначного решения, и существует много подходов к решению этой задачи. Выделяют пороговые методы, с помощью которых можно разделить изображение на разные по яркости области; подходы, основанные на разрывности яркости точек изображения, методы выделения границ и т.д.

Пороговый метод.

Разработаны разные подходы к пороговому методу. Достаточно популярно предположение, что изображение содержит известное число однородных по яркости точек или класс точек, то есть такие классы, распределение вероятности яркостей которых унимодально. Считается, что граничные области занимают небольшую площадь изображения, и пороги для сегментации могут быть расположены в межмодовых впадинах.

К сожалению, изображение реальных сцен часто плохо удовлетворяет сделанным предположениям. Кроме того, границы между отдельными областями часто размыты. Шум, присутствующий на изображении, затрудняет локализацию межмодовых впадин, что приводит к большим ошибкам в сегментации.

Дискриминантный критерий.

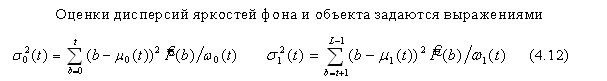
Введем понятия внутриклассовой, межклассовой и полной дисперсий.

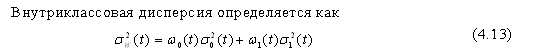
Чем меньше дисперсия класса, тем меньше будет внутриклассовая дисперсия (чем уже моды соответствующих гистограмм, тем меньше суммарная внутриклассовая дисперсия).

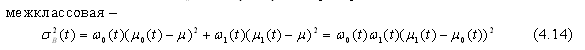
Чем дальше отстоят моды гистограммы, тем больше межклассовая дисперсия.

Ясно, что η(t) имеет минимум, равный нулю, когда ω₀(t)=0 или ω₀(t)=1, то есть, когда все точки изображения относятся либо только к объекту, либо только к фону. В диапазоне 0< ω₀(t)<1 функция η(t) принимает положительное ограниченное значение, что обеспечивает существование максимума. Описанный метод называется дискриминантным (DTSM).