101. Основные типы резьб

1)Метрическая – имеет треуголный профиль с углом альфа=60, имеются срезы профиля, что обеспечивает зазоры в соединении. Является основной крепёжной резьбой по причине наибольшей силы трения и наибольшей прочности витков на срез.

2) Трубная – угол треугольного профиля альфа=55. Профиль закруглен, что обеспечивает отсутствие зазоров в соединении. Является основой для соединения трубопровода. Вместо гайки используют термин муфта, вместо резьб стержня – труба.

3) Трапецеидальная -- профиль симметричная трапеция с углом альфа=30. Используется для передачи движения в обоих направлениях, т.е. для нереверсивных устройств.

4) Упорная – профиль несимметричная трапеция , рабочая сторона отклонена от вертикали на угол=3, нерабочая – на угол=30. Применяется при одностороннем нагружении со стороны рабочего профиля ( донкраты и т.д.)

5) Прямоугольная – профиль прямоугольный, имеет наименьшеие потери на трение, невозможно изготовит с высокой точностью, поэтому на них нет ГОСТА. Используют редко.

6) Круглая – профиль круглый с большими радиусами закруглений . Изготавливаются выдавливанием, накаткой, на тонкосменных деталях.

102. Силовые соотношения в винтовой паре при завинчивании гайки.

Развернём виток резьбы на среднем диаметре

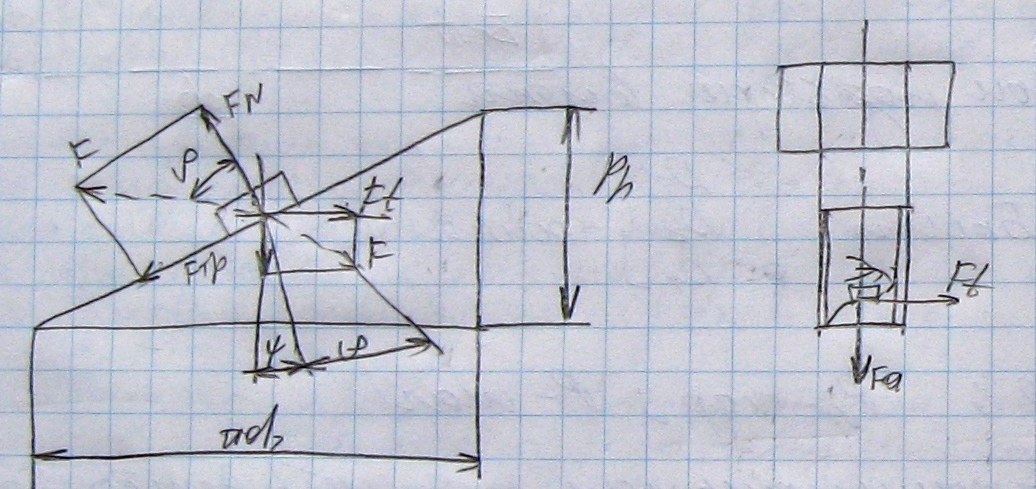
При завинчивании гайки с помощью ключа условно принимают, что к окружности d2 по касательной прикладывается движущая окружная сила Ft. При движении ползуна по наклонной плоскости вверх возникают силы:

Fтр – сила трения между ползуном и плоскостью. Fтр=fFN

При движении ползуна, сила Fтр отклоняет нормальную реакциию плоскости FN на угол g(ро) – угол трения.

Под действием сил Fтр, Fw, Ft и Fa ползун находится в состоянии равновесия. При этом Ft=Fa*tg(g+пси).

Ттр.зав.=Ft*(d2/2)=Fa(d2/2)+tg(g+пси)

Ттр.зав. – сила трения при завинчивании.

tg(g) =Fтр/FN= (FN*f)/f=f

g=arctg(f)

Ft=Fa*tg(g-пси)

103. Силовые соотношения в винтовой паре при отвинчивании гайки.

Момент сил трения в резьбе при отвинчивании гайки

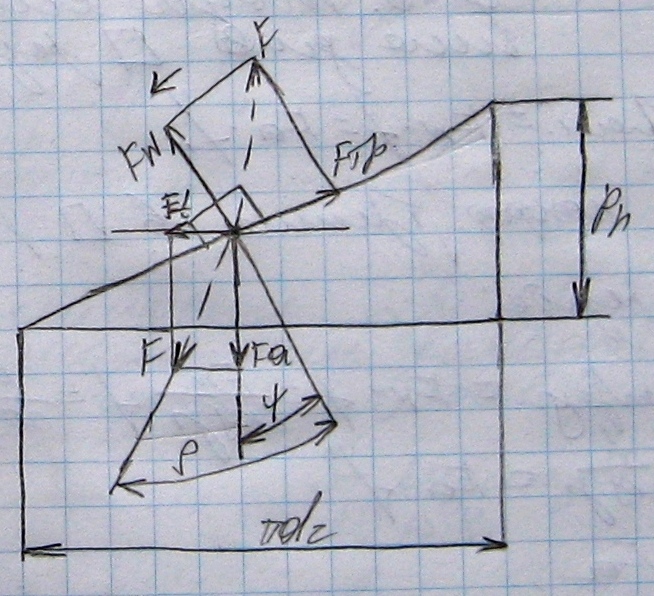
Ттр.отв.=Ft*(d2/2)= Fa(d2/2)*tg(g-пси)

Под действием осевой силы Fa ползун не может самопроизвольно сдвинуться вниз в случае Ft>0,

Fa*tg(g-пси)>0 Fa>0 всегда tg(g-пси)>0 g-пси>0 g>пси

104. Влияние профиля резьбы на силу трения в винтовой паре. Приведённый коэффициент трения и приведённый угол трения в остроугольной резьбе.

Две винтовые пары : с прямоуголной и труугольной резьбами.

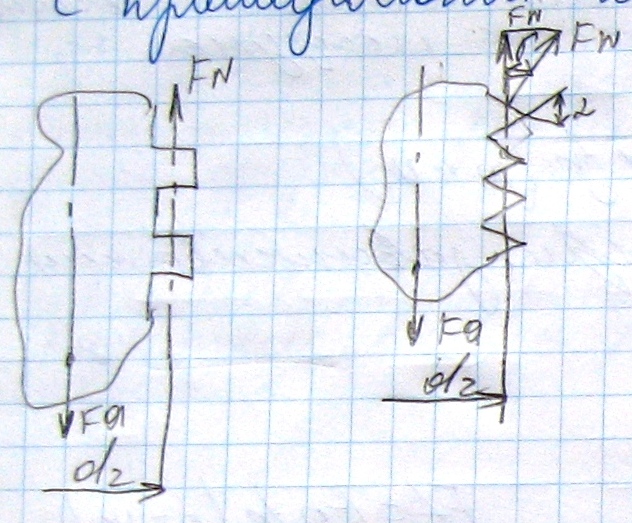
Пусть каждый из стержней нагружен одинаковой осевой статической силой Fa. При завинчивании гайки на её винтах возникает реактивная распределённая нагрузка, которую условно заменили F_N.

При пси=0. Тогда сила трения для прямойгольной резьбы :

Fтр.прям.=F_N*f=Fa*f , f-действительный коэф. трения в прямоугольной резьбе.

Сила трения в треугольной резьбе :

Fтр.треуг.=F_N*f=(F^/N / cos(гамма))*f=(Fa/cos(гамма))*f=Fa*(f/cos(гамма))=Fa*f^/

F^/N=Fa

f^/ - приведённый или фиктивный коэф. трения

f^/=f/cos(гамма)

Для треуголной резьбы(метрической) гамма=30, f^/=1,15f

Для трапецеидальной резьбы гамма=15, f^/=1,04f

Для упорной резьбы гамма=3, f^/=f

Для прямоугольной резьбы гамма=0, f^/=f

Таким образом при одинаковой нагрузке Fa наибольшая сила трения возникает в метрической резьбе треугольного профиля. А т.к. у основания витка треугольного профиля будут меньше напряжения, то метрическая резьба принята в качестве основной крепёжной резьбы.

105. Условие самоторможения винтовой пары.

Условие самоторможения в резьбе. Для стандартных резьб всегда это условие выполняется

106. Зависимость между моментом , приложенным к гайке и осевой силой винта. Момент завинчивания и отвинчивания прикладываемый к ключу.

S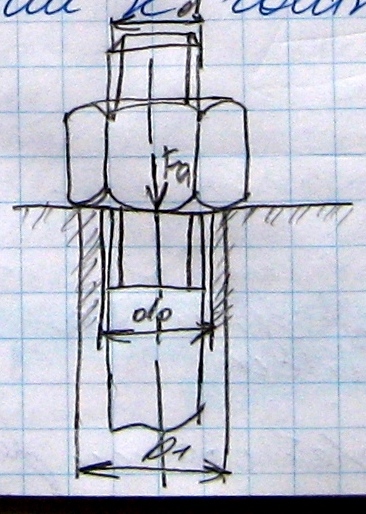 -размер под ключ.

D₁=S

Lключа=15d

V

Момент завинчивания приложенной гайки :

Тзав.=Ттр.зав.+Тт.

Ттр.зав.=Fa*(d_с/2)*tg(g^/+пси)

Тт-момент сил трения на торце гайки.

Тт=Fa*f_T(d_ср/2)

f_T –коэффициент трения на торце гайки.

d_ср- средний диаметр на площадке трения

d_ср=(D₁+d₀)/2, тогда Тзав.=(Fa/2)*(tg(g^/+пси)*d_c+f_T*d_ср)

107. КПД винтовой пары

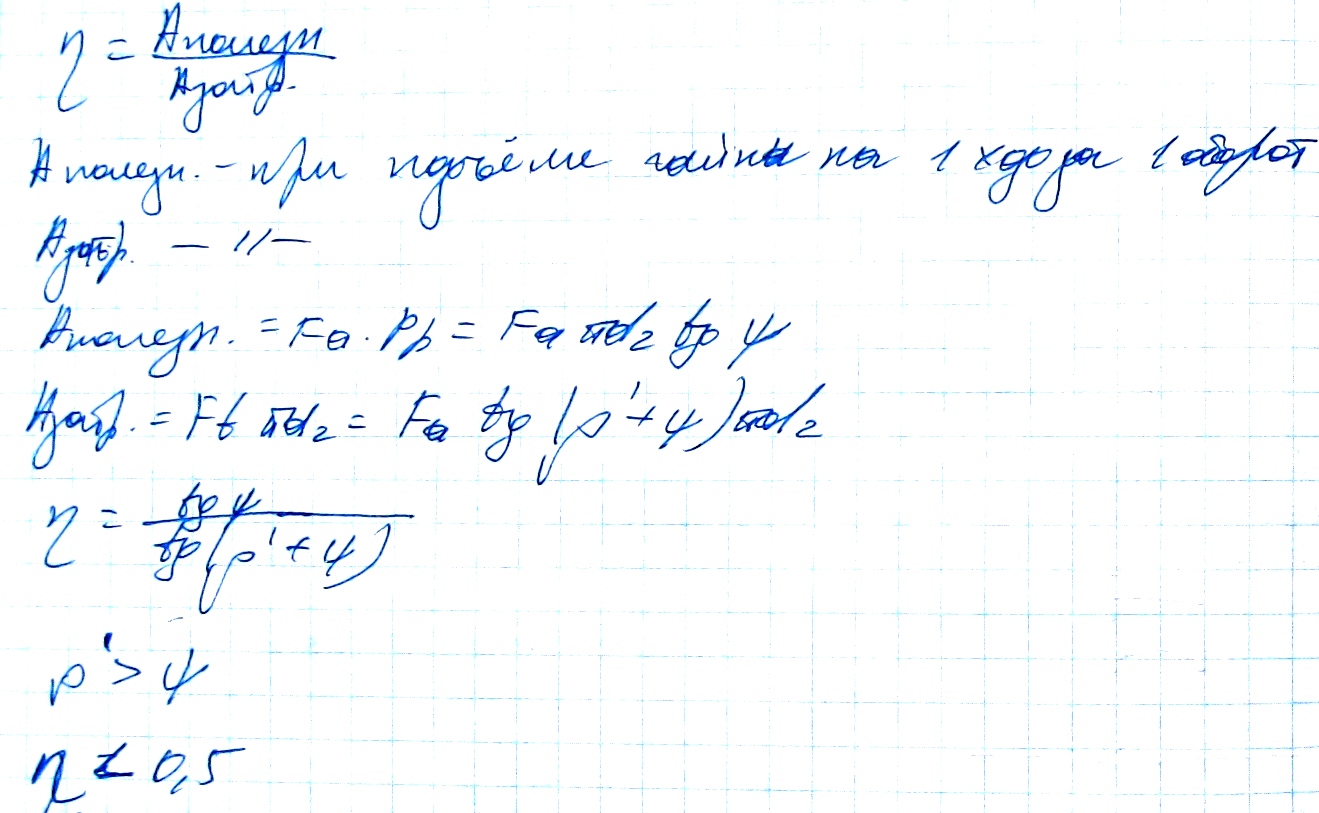
108. Распределение осевой нагрузки по виткам резьбы гайки.

Данную задачу впервые теоретически решил Н.Е. Жуковский. Он установил, что на первый виток резьбы гайки от опорной поверхности приходится примерно 1/3 Fa, а на десятый примерно 1/100 Fa.

Данный вывод был подтверждён экспериментально. Результаты этих исследований учитывают при выборе высот гаек.

109. Классы прочности резьбовых деталей.

Для болтов, винтов и шпилек установлено 12 классов прочности, а для гаек 7. Для средних нагрузок и общего машиностроения основными являются классы прочности: болты, винты, шпильки :

5.6 ; 5.8; гайки 6

6.6 ; 6.8 ; 8

Для гайки класс прочности показывает тот наибольший класс прочности болта, с которым данная гайка может свинчиваться. Пример : гайка6 -- использовать болт не выше 6.8.

Обозначение болтов. Болт М12-6gx60.66.05 ГОСТ

60 – длина болта до головки болта

66-класс прочности (без точки)

05-покрытие

Для стержных винтов корпусов редуктора, а также для привёртных подшипниковых крышек рекомендуются болты не ниже класса прочности 6.6