- •Экзамен по начертательной геометрии
- •1. Метод проецирования. Центральное и параллельное проецирование.
- •2. Чертеж точки в сне теме прямоугольных координат. Способы
- •3. Прямая линия общего и частного положения на эпюре
- •4. Следы прямой линии. Сформулировать последовательность построения горизонтальною и фронтального следов прямой.
- •5. Определение истинной величины отрезка прямой общего положения способом прямоугольного треугольника.
- •6. Взаимное положение точки и прямой, двух прямых. Определение видимости проекций точек на скрещивающихся прямых.
- •8. Горизонтали и фронтали плоскости. Точка и прямая в плоскости.
- •9. Взаимное положение прямой и плоскости (прямые параллельные и перпендикулярные плоскости). Проецирование прямого угла.
- •10. Взаимное положение двух плоскостей. Построение линии пересечения плоскостей при различных способах их задания.
- •11. Правила построения точки пересечения прямой с плоскостью. Определение видимости прямой.
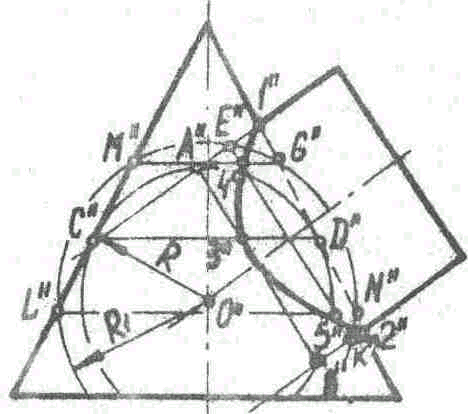
- •12. Аксонометрические проекции. Основные понятия и определения. Построение окружности в аксонометрических проекциях.
- •13. Стандартные виды аксонометрических проекций. Коэффициенты искажения. Построение окружности в аксонометрических проекциях.
- •15. Способ замены плоское! ей.
- •16. Способ врящсния вокруг проецирующих прямых.
- •18. Развертки поверхностен. Развертывание поверхности многогранников.
- •19. Пересечение кривых поверхностей плоскостью частною положения. Линии конических сечений.
- •24. Линейчатые поверхности (развертываемые и неразвертываемые). Нелинейчатые поверхности.
- •26. Построение линии взаимною пересечения многогранных поверхностей.
- •29.Особые случаи пересечения поверхностей вращения.
- •30. Построение .Пшии персе', чения поверхностей способом концентрических вспомогательных
24. Линейчатые поверхности (развертываемые и неразвертываемые). Нелинейчатые поверхности.
25. Построение точки ik •pi '.ч •чения прямой с поверхностью (общий случай). Способы построения точек пересечения np«Miii; с поверхностью.
^* Через прямую пронес ш вспомогательную плоскость
<•» Определить линию пересечения вспомогательной плоскости с заданной поверхностью »> Определить искомые точки (входа и выхода) как результат пересечения заданной прямой с найденной линией перессчсня *t* Определить видим осп,


26. Построение линии взаимною пересечения многогранных поверхностей.
Линия пересечения двух многогранников — замкнутая пространственная ломаная линия. При ее построении используют два способа.
1. Определяют точки. г> которых ребра одной поверхности пересекают грани второй и ребра второй пересекают грани iicp^iii (задача на пересечение прямой с плоскостью). Через найденные точки в определенной последовательности проводят линию. При этом можно соединять прямыми проекции точек, лежащих в одной грани.
2. Определить отрезки, по ко торым грани одной поверхности пересекают грани второй (задача на
пересечение двух плоскостей).
Если проекция ребра одною из многогранников не пересекает грани второго хотя бы на одной из проекций, то это ребро не пересекает эту грань.
27. Построение линии вз.и^ ного пересечения поверхностей вращения. Выбор секущих плоскостей.

28. Способ вспомо! атслы!1,1.\ секущих плоскостей.

29.Особые случаи пересечения поверхностей вращения.
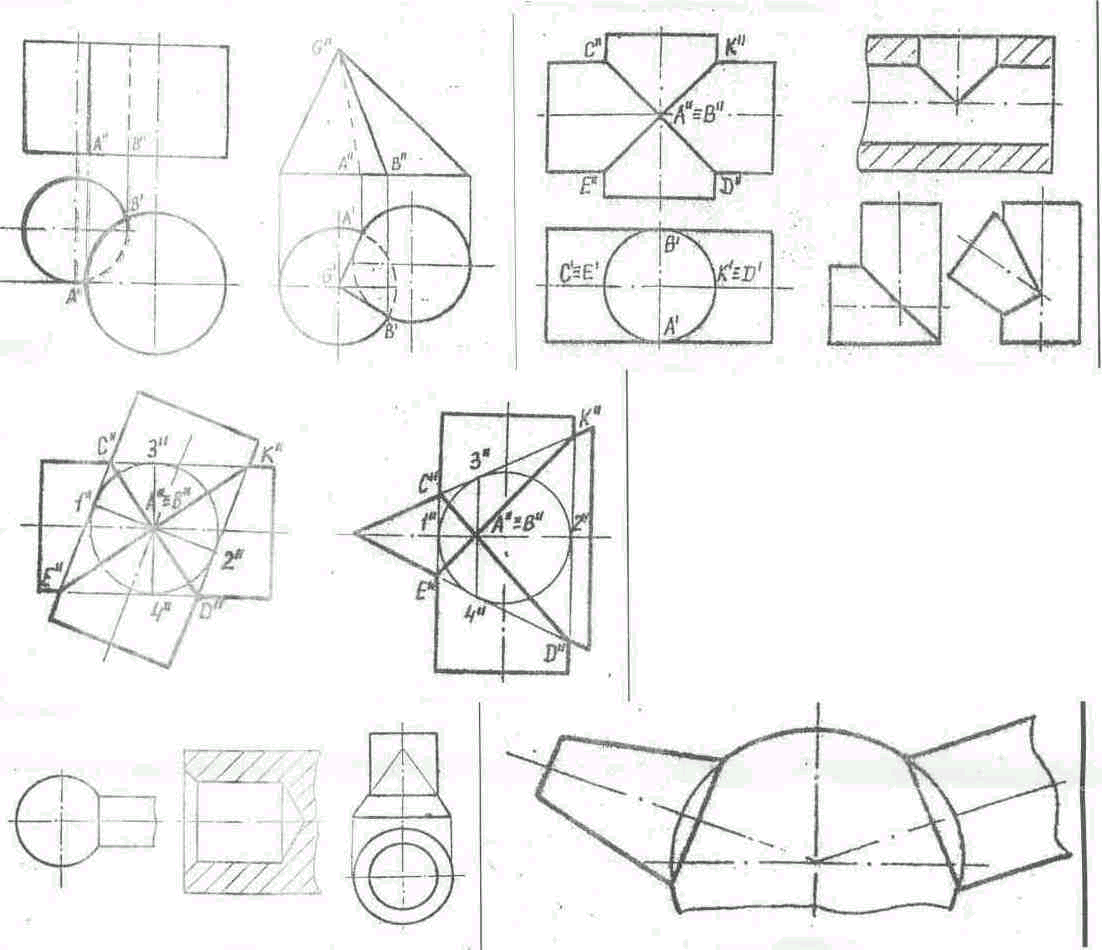
30. Построение .Пшии персе', чения поверхностей способом концентрических вспомогательных
сфер.
Способ коицен трнческих вспомогательных сфер возможно использовать при следующих условиях: пересекаю |циеся поверхности - поверхности вращения; оси этих поверхностей должны пересекаться;
плоскость осей должна быть параллельна одной из плоскостей проекций.